如今的深度神经网络已经具有了完备的能力,特别是在视觉领域已经接近甚至超过了人类的视觉能力,而在这些深度学习网络的背后都含有着一个基本框架,即卷积神经网络(CNN)。CNN的主要应用范围是在计算机视觉领域,这里我简单的介绍一下CNN中的经典模型AlexNet。AlexNet是由Alex Krizhevsky等人在2012年提出的,虽然现在这个模型已经比较少见了(大多数都使用resnet什么的),这个在当时的目标检测领域有着很好的表现,也为后续的其它CNN框架奠定了基础。
介绍
为了从几百万张图片中学会识别几千个目标对象,Krizhevsky等人构建了一个具有强学习能力的模型,同时考虑到在某些目标识别任务上巨大的复杂性并不能通过增大数据集来解决,而是需要一定量的先验知识来补充模型。卷积神经网络模型的能力可以通过深度和宽度来控制,同时它也能准确捕捉到统计的平稳性和像素区域的局部性这两个自然图像规律,所以用CNN进行图像识别是个不错的选择。
基本框架
不多bb,直接上截图:
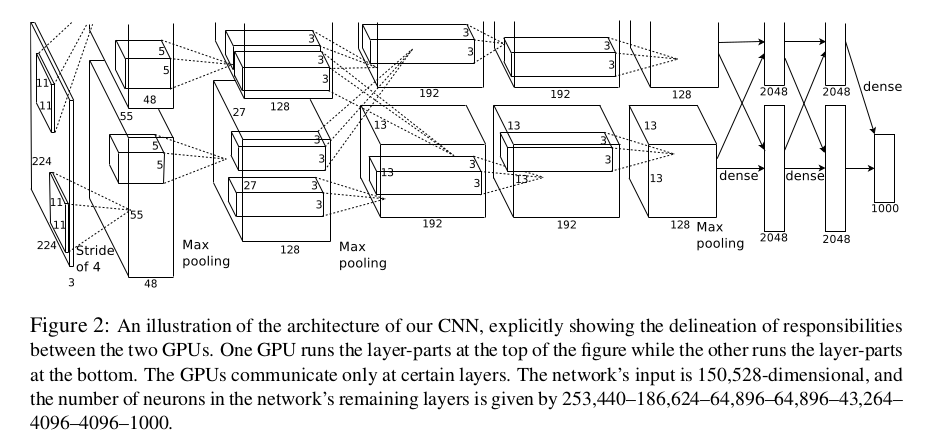
这个框架包含了8个学习层(5个卷积层和3个全连接层),由于受到GPU显存的限制,作者在两个GPU上运行,最后再将运行数据合并再一起,这实际上就是分组卷积的操作。模型中第二、四、五卷积层中的核只跟在同一侧GPU上的上一卷积层有联系,第三层卷积层连接了第二层卷积层的所有核。响应标准化层在第一以及第二卷积层之后。最大池化层位于响应标准层和第五层之后,ReLU激活函数应用于每一个卷积层和全连接层中。模型的目标为最大化多项逻辑回归目标函数。接下来是对模型使用的一些特殊技巧进行说明。
激活函数
在2012年,神经网络的激活函数使用最多的是\(f(x) = tanh(x)\)或者\(f(x) = (1+e^{-x})^{-1}\),而作者采用的是现在使用十分广泛的ReLU激活函数(\(f(x) = max(0,x)\)),这个是不饱和非线性函数,它的下降速度快于之前两个饱和非线性函数,这让深度卷积神经网络在ReLU激活函数下的工作效率有了几倍的提升。
不饱和非线性函数:非线性即是平常所说的非线性,而不饱和是指当变量x趋于无穷是,函数的取值也趋于无穷。
局部响应标准化
ReLUs有一个非常好的属性,即它不需要输入规范化以防止它们饱和。但作者仍然使用了如下的归一化:
\[ b^i_{x,y} = \frac{a^i_{x,y}}{\left(k+\alpha\sum^{min(N-1,i+n/2)}_{j=max(0,i-n/2)}{(\alpha^j_{x,y})^2}\right)^{\beta}} \]
其中\(b^i_{x,y}\)表示响应的标准化神经元激活程度,\(\alpha^i_{x,y}\)为在位置\((x,y)\)处应用核\(i\)和ReLU非线性激活函数的神经元的激活程度,\(N\)是层中的总核数,求和操作遍历了同一空间位置上的核映射。核映射的顺序是随意的,在训练开始时才决定,这种方式实现了一种横向抑制,即在使用不同内核计算的神经元输出之间创建大活动的竞争。
关于超参数的选用,作者选择的超参数为:\(k=2\),\(n=5\),\(\alpha=10^{-4}\)以及\(\beta=0.75\)。
重叠池化
CNN中的池化层是对同一内核映射相邻组神经元的输出进行统计总结的操作。通常的池化操作通过相邻的池化单元来完成操作具体,来说池化层可以看作是由间隔S个像素的合并单元格组成,合并单元格统计了以该单元格为中心的\(Z \times Z\)邻域。如果令\(S = Z\),我们就得到了传统的卷积神经网络池化操作;对于\(S < Z\),我们可以得到重叠池化操作。作者选用的参数为\(S = 2\),\(Z = 3\)。具有重叠池化的模型在训练期间过度拟合会稍微困难一些。
降低过拟合
数据增强
降低过拟合的简便的常用操作就是进行数据增强以增加数据集。在论文里,作者采用的增强手法主要是图像平移水平反射和改变训练图像中RGB通道的强度。
首先是图像平移水平反射,作者随机地从\(256 \times 256\)的图像中提取出\(224 \times 224\)的块以及对应的水平反射块。然后再用这些数据对模型进行训练。在预测阶段,模型使用五个\(224 \times 224\)的数据块(四个角落和一个中心)以及它们的水平反射块,即一共10个数据块进行预测,最后将预测结果通过\(softmax\)层进行统计得到最终预测结果。
对于改变训练图像中的RGB通道的强度这一方法,作者将\(PCA\)算法应用于图像训练集的RGB通道像素值集上。对于每个训练图像,我们添加多个找到的主成分,其幅值与相应的特征值成正比乘以从均值为0,标准差为0.1的高斯图形中取得的随机变量值。所以每个RGB像素值\(I_{xy} = [I^R_{xy},I^G_{xy},I^B_{xy}]\),添加了以下的权值:
\[ [\mathbf{p}_1,\mathbf{p}_2,\mathbf{p}_3][\alpha_1\lambda_1,\alpha_2\lambda_2,\alpha_3\lambda_3]^T \]
其中\(\mathbf{p}_i\)和\(\lambda_i\)是\(3 \times 3\)的RGB像素值协方差矩阵第\(i\)个特征向量和特征值,\(\alpha_i\)是上面提到的随机变量,对于特定训练图像的所有像素,每个\(\alpha_i\)的值仅取一次,直到该图像被重新用于训练,此时\(\alpha_i\)将被会再去一次值。这种方法大致的捕捉到了自然图像的属性,即对象身份对于照明的强度和颜色的变化是不变的。
Dropout
以一定的概率(作者选用0.5)将某个隐藏层神经元的输出设置为0,此时被设置为0的神经元对前向传播没有贡献同时也不会受到误差反向传播的影响,即神经结构发生了变化。这项技术减少了神经元复杂的共同适应,因为神经元不能依赖于特定的其他神经元。作者选用的Dropout概率0.5是由指数多个dropout网络产生的预测分布的几何平均值。dropout操作大概使得模型收敛所需的迭代次数加倍。
一些训练细节
优化方法为SGD,其中batch size为128个,动量参数设置为0.9并且权值衰减参数设置为0.0005。作者发现少量的权值衰减对模型的学习很重要。对于权值的更新如下:
\[ \begin{aligned} \mathbb{v}_{i+1} & := 0.9\cdot\mathbb{v}_i-0.0005\cdot\epsilon\cdot\mathbb{\omega}_i-\epsilon\cdot\left\langle\frac{\partial{L}}{\partial{\mathbb{\omega}}}\vert_{\mathbb{\omega}_i}\right\rangle_{D_i} \\ \mathbb{\omega}_{i+1} & := \mathbb{\omega}_i+\mathbb{v}_{i+1} \end{aligned} \]
其中第一个等式的最后一项偏导数取值为模型在第\(i\)个批次中\(D_i\)的损失对\(w\)的偏导数在\(w_i\)处的值的平均值,\(i\)是迭代次数索引,\(v\)是动量变量,\(\epsilon\)是学习率。
使用均值为0,标准差为0.01的高斯分布对模型权值进行初始化,初始化模型第二、四、五卷积层以及隐藏层的全连接层的偏差值为常数1,这会通过向ReLU提供正输入来加速学习的早期阶段,剩余的神经元偏差值设置为0。对于所有层,作者使用了相同的学习率(0.01)并在训练中进行调整,当在当前的学习率下验证集的错误率不再下降时,将学习率除以10,学习率下调三次后则停止训练。
总之,AlexNet这个网络模型在2012年的ImageNet竞赛上取得了相当不错的成绩,其中Top-5错误率降低到了\(15.3\%\)。这个模型可以说是入门深度学习视觉领域的一个非常经典的模型,里面用到的许多技巧在后续的模型发展中也有很好的应用。
致谢
本文参考自Alex Krizhevsky等人于2012年发表的论文:
ImageNet Classification with Deep Convolutional Neural Networks