首先祝所有教师节日快乐,感谢你们赠人玫瑰手留余香的奉献精神。然后时隔将近一个月,我又滚回来更新博客了,之前一直在忙着入职这件事,希望能尽快融入公司开发业务中而”忙碌“了一个月。接下来继续经典图像识别网络模型的介绍。上文我们已经介绍了AlexNet和VGG网络,这两个网络都将当时的神经网络的深度发挥到了极致,后续的神经网络模型性能基本上好不了多少。这是由于随着网络的加深,在误差后向传播时,靠前的网络层权重基本得不到更新,一直维持在某一个值附近。在2015年,何凯明大神提出了一种快捷连接方式将误差传播到了前面的网络层,很大程度上提高了网络的性能。下面简单解析一下ResNet网络。
快捷连接
神经网络层数的增多理论上应该会得到性能更好的模型,但由于梯度消失的存在,限制了网络层数的发展。为此,何凯明大佬提出了一种网络结构单元解决了梯度无法传递到网络底层的问题,那就是快捷连接。基本结构如下图所示:

这种结构其实是一种残差网络。其中\(x\)表示这一结构单元的输入,\(\mathcal{H}(x)\)表示结构单元的映射函数。假设多层非线性网络结构可以拟合任何复杂函数,也即是说这种结构可以拟合残差函数\(\mathcal{H}(x)-x\),所以与其去拟合原映射函数\(\mathcal{H}(x)\)不如拟合残差函数\(\mathcal{F}(x) := \mathcal{H}(x)-x\),因为拟合原函数还是避免不了梯度消失这一现象,同时从图中可以看出实现残差函数的方式十分简单。
在快捷连接中有一个十分重要的组成部分,就是\(Identity \ Mapping\),上图的连接单元可以表示为:\(y = \mathcal{F}(x,\{\mathcal{W}_i\})+x\),其中\(x\)和\(y\)分别表示单元的输入和输出(在激活函数之前),\(\mathcal{F}(x,\{\mathcal{W}_i\})\)表示残差单元学习的函数映射。对于上图展开表示即是:\(\mathcal{F} = W_2\sigma(W_1x)\),\(\sigma\)表示\(ReLU\)激活函数,这里忽略偏差值。这种连接并没有引入额外的参数,没有增加模型的计算量。这里有个注意点,\(x\)和\(\mathcal{F}\)的输出必须具有相同的维度,若不相同,可以通过线性修正\(W_s\)来同步维度:\(y = \mathcal{F}(x,\{\mathcal{W}_i\})+W_sx\)。
基本结构
作者针对\(ImageNet\)的数据集设置了三组网络模型,以此为例来解说\(ResNet\)的结构
普通的卷积神经网络
基本网络的设计大都来源于\(VGG\)网络,卷积层的卷积核大小基本为\(3 \times 3\)并且遵循以下两个简单的设计原则:
- 对于具有同样输出的网络层,都设置相同数量的卷积核;
- 若特征图的大小减半,设置加倍的卷积核数量以减少每一层的计算复杂度
对于具有2步幅的卷积层,作者直接对该层进行下采样操作。整体网络以全局平均池化层和1000路带\(softmax\)的全连接层。网络模型的权重层数为\(34\)。
带残差单元的卷积神经网络
基于之前设计普通神经网络添加快捷连接来进行更改。快捷连接可以直接使用在连接前后的维度相同的情况下,而对于维度不同的情况,有以下两种处理方法:
- 用零填充来扩展维度进行匹配,该方法不引入额外参数;
- 使用\(1 \times 1\)的卷积核来扩展维度
具体结构图如下:
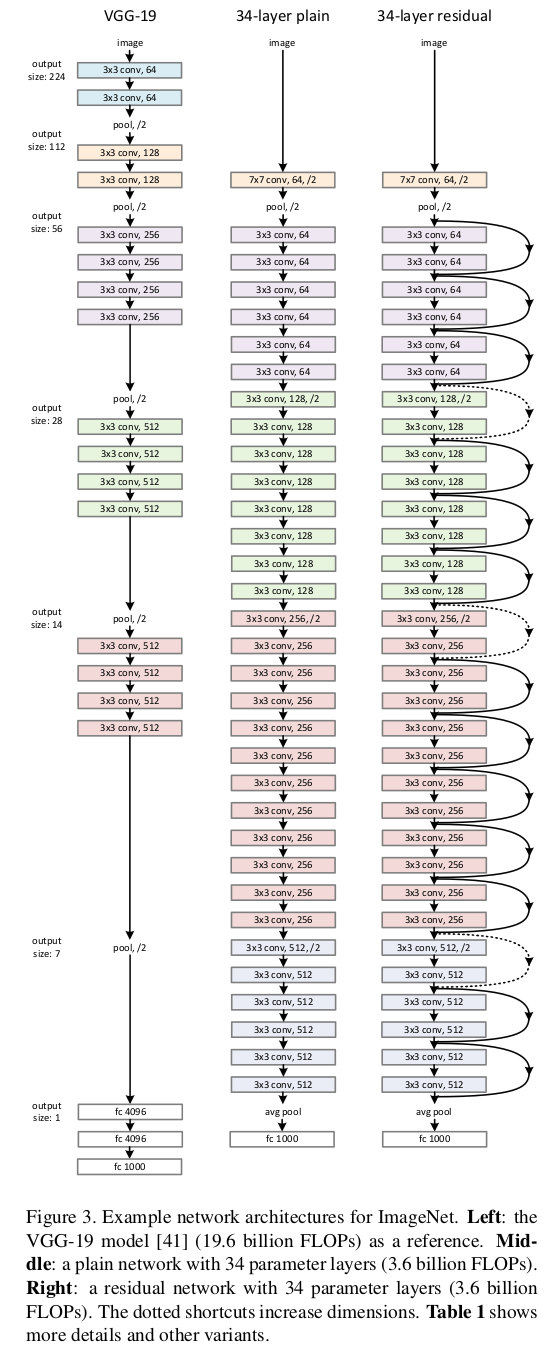
其中左边为\(VGG\)网络(用来作参考),中间即为普通的卷积神经网络,右边为带残差单元的卷积神经网络,虚线的快捷连接表示连接过程中增加维度。
后续的实验中作者也采用了许多\(ResNet\)网络的变种,具体结构如下:
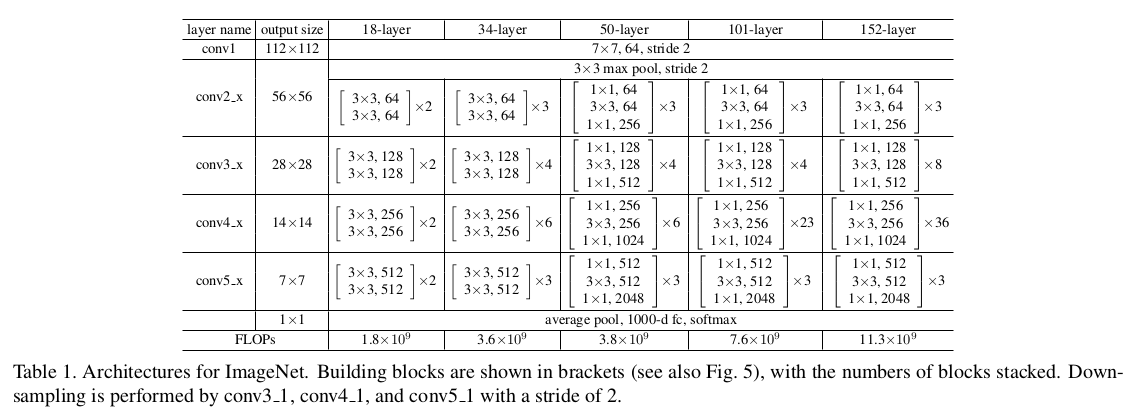
Identity Mapping
作者在推出\(ResNet\)这篇论文不久后,就发了一篇关于\(ResNet\)网络快捷连接中\(Identity \ Mapping\)数学原理的论文来进一步证实该模型的可靠性。这里进行一个大致解析。
残差单元可以表示为如下形式:
\[ \begin{aligned} y_l & = h(x)+\mathcal{F}(x_l,\mathcal{W}_l) \\ x_{l+1} & = f(y_l) \end{aligned} \]
其中\(x_l\),\(x_{l+1}\)为第\(l\)个残差单元的输入和输出,\(\mathcal{F}\)为残差函数,\(f\)为\(ReLU\)激活函数,其中\(\mathcal{W}_l\)表示如下:
\[ \mathcal{W}_l=\{W_{l,k}\vert 1\le k\le K\} \]
\(l\)是第\(l\)个单元的权重(包含偏差值),\(K\)是残差单元中的网络层数。
为了证明\(Identity \ Mapping\)选择的正确性,这里作者做了分类假设,且为了简化分析还将\(f\)函数进行了统一(均为\(Identity \ Mapping\)),即有\(x_{l+1}=y_l\)。
设\(h(x_l)=x_l\),即\(Identity \ Mapping\)
由假设可以得到:
\[ x_{l+1} = x_l+\mathcal{F}(x_l, \mathcal{W}_l) \]
递归有:
\[ \begin{aligned} x_{l+2} & = x_{l+1}+\mathcal{F}(x_{l+1},\mathcal{W}_{l+1}) \\ & = x_l+\mathcal{F}(x_l,\mathcal{W}_l)+\mathcal{F}(x_{l+1},\mathcal{W}_{l+1}) \\ & = \dots \end{aligned} \]
化简可得:
\[ x_L = x_l+\sum_{i=1}^{L-1}\mathcal{F}(x_i,\mathcal{W}_i) \]
这形式有两个好处:
- 任意深度的残差单元的特征\(x_L\)可由任意浅层的残差单元\(l\)加上残差项\(\sum_{i=1}^{L-1}\mathcal{F}\)表示,即模型在任何单元\(L\)和\(l\)之间处于残余方式;
- 对任意深度的残差单元\(L\),式子\(x_L = x_0+\sum_{i=0}^{L-1}\mathcal{F}(x_i,\mathcal{W}_i)\)都是对前面所有残差函数的输出进行求和,与普通网络模型的矩阵向量求积不同
(补充:普通网络模型的矩阵向量求积式为:\(x_L=\prod_{i=0}^{L-1}\mathcal{W}_ix_0\))
该形式对后向传播也有十分良好的性能,假设\(\epsilon\)为损失函数,则有:
\[ \begin{aligned} \frac{\partial{\epsilon}}{\partial{x_l}} & = \frac{\partial{\epsilon}}{\partial{x_L}}\cdot\frac{\partial{x_L}}{\partial{x_l}} \\ & = \frac{\partial{\epsilon}}{\partial{x_L}}\left(1+\frac{\partial{}}{\partial{x_l}}\sum_{i=1}^{L-1}\mathcal{F}(x_i,\mathcal{W}_i)\right) \end{aligned} \]
其中\(\frac{\partial{\epsilon}}{\partial{x_L}}\)的传播不通过权重层而直接进行传播,另外一项的传播则通过权重层。对于\(\frac{\partial{}}{\partial{x_l}}\sum_{i=1}^{L-1}\mathcal{F}(x_i,\mathcal{W}_i)\)对一个\(minibatch\)中的样本并不会总是为-1,即不会出现梯度消失现象(因\(\frac{\partial{\epsilon}}{\partial{x_l}}\)不会为零)。
设\(h(x_l)=\lambda_lx_l\),\(\lambda_l\)为调制参数
同样由假设可以得到\(x_{l+1}=\lambda_lx_l+\mathcal{F}(x_{l},\mathcal{W}_{l})\),递归可得
\[ x_L=(\prod_{i=1}^{L-1}\lambda_i)x_l+\sum_{i=1}^{L-1}(\prod_{j=i+1}^{L-1}\lambda_j)\mathcal{F}(x_i,\{\mathcal{W}_i\}) \]
进行化简可以得到下式:
\[ x_L=(\prod_{i=l}^{L-1}\lambda_i)x_l+\sum_{i=1}^{L-1}\hat{\mathcal{F}}(x_i,\mathcal{W}_i) \]
其中\(\hat{\mathcal{F}}(x_i,\mathcal{W}_i)\)将标量包含在里面。对上式进行后向传播时有:
\[ \frac{\partial{\epsilon}}{\partial{x_l}} = \frac{\partial{\epsilon}}{\partial{x_L}}\left((\prod_{i=l}^{L-1}\lambda_i)+\frac{\partial{}}{\partial{x_l}}\sum_{i=l}^{L-1}\hat{\mathcal{F}}(x_i,\mathcal{W}_i)\right) \]
当网络很深时(\(L\)很大),若对于所有的\(i\)都有\(\lambda_i \lt 1\),则因子\(\prod_{i=l}^{L-1}\lambda_i\)会呈现出爆炸式增长;若对于所有的\(i\)都有\(\lambda_i \gt 1\),则因子\(\prod_{i=l}^{L-1}\lambda_i\)会变得非常小甚至为零,这些都会阻碍网络的学习。
激活函数的选取
上面论证了\(Identity \ Mapping\)的重要性,而这是基于一个重要的假设,即激活函数\(f\)为\(Identity \ Mapping\),所以接下来作者对激活函数使用其它形式的情况进行了讨论。具体细节图如下:
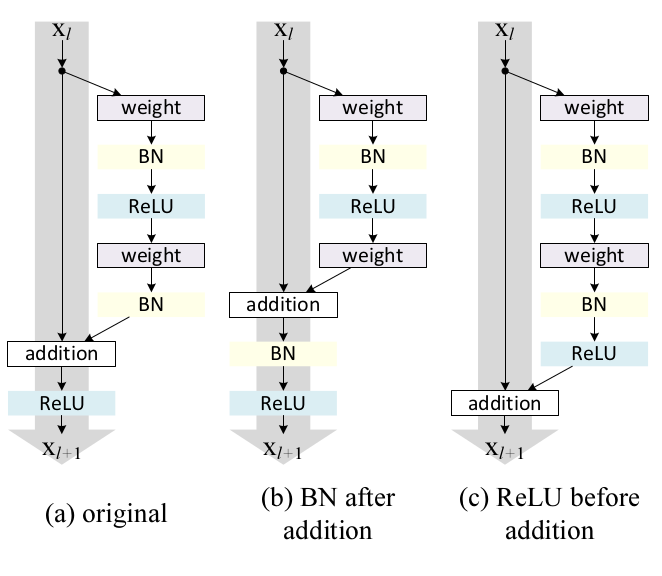
图中\(a\)是参考单元,保留了原来的结构,激活函数只有\(ReLU\);\(b\)将\(BN\)层放在了相加操作之后,即激活函数包括了\(BN\)层和\(ReLU\),经过作者实验,这种结构的表示能力不及原先结构的强,该结构中\(BN\)层会影响信息的传输;\(c\)则将\(ReLU\)放在了相加操作之前,激活函数就变成了\(Identity \ Mapping\),但这导致函数\(\mathcal{F}\)的输出为非负的,而直观上函数\(\mathcal{F}\)应该在\((+\infty, -\infty)\)上取值,所以结果是残差单元前向传播信号会有单调递增,影响模型表达能力。
残差单元的改进
对于原先的结构,有:
\[ \begin{aligned} y_l & = h(x_l)+\mathcal{F}(x_l,\mathcal{W}_l) \\ x_{l+1} & = f(y_l) \end{aligned} \]
对于下一个单元,有:
\[ \begin{aligned} y_{l+1} & = h(x_{l+1})+\mathcal{F}(x_{l+1},\mathcal{W}_{l+1}) \\ & = x_{l+1}+\mathcal{F}(x_{l+1},\mathcal{W}_{l+1}) \\ & = f(y_l)+\mathcal{F}(f(y_l),\mathcal{W}_{l+1}) \end{aligned} \]
从式中可以看出函数\(x_{l+1}=f(y_l)\)影响了本单元以及下一单元。
作者提出了一种非对称结构解决了这个问题,具体结构如下:
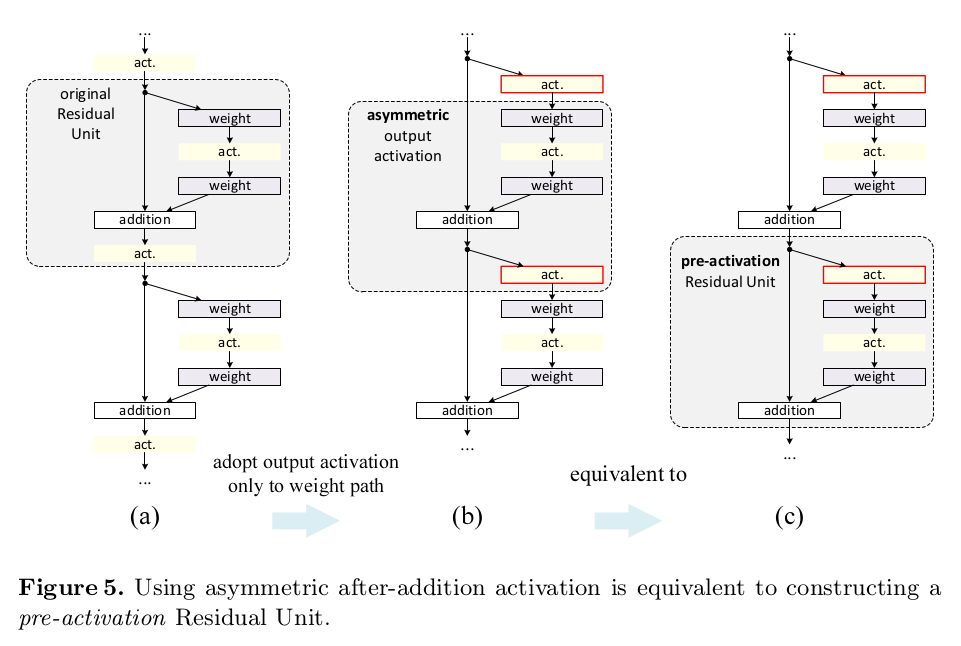
表示如下:
\[ x_{l+1} = x_l+\mathcal{F}(\hat{f}(x_l), \mathcal{W}_l) \]
从图中也可以看出\(post-activation\)和\(pre-activation\)是等价的,数学表达式与\(x_L = x_l+\sum_{i=1}^{L-1}\mathcal{F}(x_i,\mathcal{W}_i)\)相似,故反向传播形式也类似,即没有梯度消失或爆炸现象,同时上面结构中激活函数为\(Identity \ Mapping\)形式。
改进后激活函数的位置选取
对于改进后的残差单元激活函数位置的选取,作者考虑了两种结构,如下:
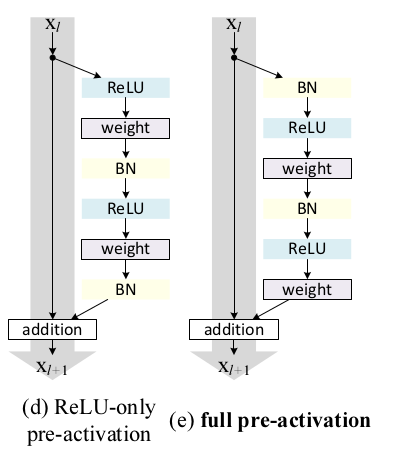
实验表明,\(e\)图所示结构取得了较其它优秀的性能,主要有两方面的原因:
- 激活函数为\(Identity \ Mapping\)。作者在实验中发现快捷连接单元中的\(h(x_l)\)与激活函数\(f\)越接近\(Identity \ Mapping\)时,模型表示能力越好;
- 在pre-activation中使用\(BN\)层提升了模型正则化能力,原先结构虽然也有\(BN\)层进行正则化,但之后又加上了快捷连接传递过来的值,所以整个单元的输出没有经过正则化,而pre-activation对单元的输入与输出都进行了正则化。
同时该结构易于优化,原先结构单元的激活函数\(f=ReLU\)在负数情况下会影响信号传播,而且这种影响会随这残差单元数量的增长而加强。改进的结构单元的激活函数采用的是\(Identity \ Mapping\),可以直接将误差传播到下一层。
致谢
本文参考自何凯明大佬在2015和2016年发布的两篇论文: