哈,难得这几天比较空闲,就抓紧总结一下之前看过的RCNN系列的论文,这篇是这一系列的第二篇。作者Ross Girshick看不惯自己曾经提出的模型(RCNN)运行起来如此之慢,所以提出了一个改进模型(Fast RCNN),接下来对该模型进行一个简单的分析。
RCNN的缓慢
与图像识别任务相比,目标检测由于需要多一个定位对象位置这一步所以难度提升了不少,其中主要解决的问题有两个,一个是模型需要大量的对象候选框;另外一个是这些候选框只是粗略地提供了对象的大概位置,需要模型去做一个回归的操作。\(RCNN\)是一个多阶段训练模型。\(RCNN\)模型首先在对象候选框上使用对数损失来微调卷积神经网络,然后得到的特征图传给\(SVM\)进行目标分类,这些\(SVM\)代替了需要微调的\(softmax\)层,在第三训练阶段,模型学习边界框回归。对于\(SVM\)和边界框回归的训练,\(RCNN\)将每个目标候选框的特征都写入了磁盘中,这无疑耗费了十分巨大的时间和空间,其次,目标识别的速度过慢,在GPU上识别图片大概需要47秒每张图片。\(RCNN\)缓慢还有一个重要原因,即模型没有共享卷积层的计算。
基本结构
\(Fast \ RCNN\)是一个单阶段训练的模型。它将整个图像和一组候选框都作为输入,模型首先用一组卷积层和最大池化层对整张图像进行特征提取,再在提取出的特征图上,针对每一个候选框用\(RoI \ pooling\)池化层提取出一个固定长度的特征向量,之后送入全连接层最终分成两个分支分别进行目标识别和边界框回归。具体框架如下:
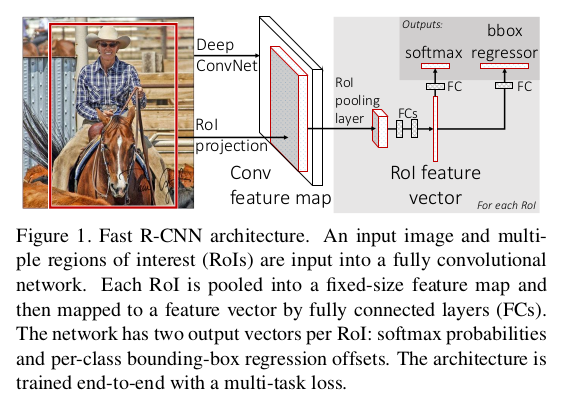
\(RoI \ pooling\)将\(h \times w\)的\(RoI\)区域划分为\(h/H \times w/W\)规格的子窗口,再在各个子窗口上应用\(max \ pooling\)从而输出一个固定长度的特征向量。
预训练和微调网络
对于网络的初始化,作者使用了三个预训练的\(ImageNet\)的模型,并进行了如下更改:
- 原网络最后一个\(max \ pooling\)层用\(RoI \ pooling\)层替代并指定参数\(H \times W\)以适应网络的第一个全连接层的尺寸;
- 原网络最后一个全连接网络和\(softmax\)层替代为两个分支网络;
- 原网络修正为两个输入
作者提出了一个包含了特征共享优势的高效模型训练方法。在\(Fast \ Rcnn\)训练中,对随机梯度下降的\(minibatch\)进行分层采样,首先采样\(N\)个样本然后从每一个样本中采样\(R/N\)个\(RoI\)。来自同一个图片的\(RoI\)共享前向以及后向传播中的计算和内存。
模型采用的损失函数为多任务损失函数。\(Fast \ RCNN\)有两个输出层,一个是输出每一个\(RoI\)的关于\(K+1\)个类的概率\(p=(p_0,\dots,p_K)\),另一个是输出边界框关于\(K\)个类的回归偏移量\(t^k=(t_x^k,t_y^k,t_w^k,t_h^k)\)。每个\(RoI\)被真实类别\(u\)和真实类别的目标框\(v\)标记。作者对每一个被标记的\(RoI\)使用多项任务损失函数\(L\)来共同训练分类和边界框回归:
\[ L(p,u,t^u,v) = L_{cls}(p,u)+\lambda[u \ge 1]L_{loc}(t^u,v) \]
其中\(L_{cls}(p,u)=-logp_u\)是对数损失,第二项损失由真实类别的回归框\(v=(v_x,v_y,v_w,v_h)\)和预测的回归框\(t^u=(t_x^u,t_y^u,t_w^u,t_h^u)\)组成的,\(L_{loc}\)忽略背景\(RoI\)类,所以对于边界框回归有:
\[ L_{loc}(t^u,v) = \sum_{t \in \{x,y,w,h\}} smooth_{L_1}(t_i^u-v_i) \]
对于\(smooth\)函数有:
\[ smooth_{L_1}(x) = \begin{cases} 0.5x^2 &\text{if $\vert x \vert\lt 1$} \\ \vert x \vert-0.5 \ &\text{otherwise} \end{cases} \]
这里采用\(L_1\)损失与\(RCNN\)采用的\(L_2\)相比少了些敏感性。多项任务损失函数中的超参数\(\lambda\)控制着两个单一损失函数的平衡。作者在论文的实验中对真实实例的边界框进行了标准化(使其均值为0,方差为1),损失函数中的超参数选为1。
关于\(minibatch\)的采样这里就不再细讲,具体可看看作者的论文。接下来说一下\(RoI \ pooling\)池化层的后向传播。令\(x_i \in R\)为\(RoI \ pooling\)的第i个输入,\(y_{rj}\)为第r个\(RoI\)的第j个输出,则\(RoI \ pooling\)的计算公式可以表示为
\[ y_{rj}=x_{i^*(i,j)} \]
其中\(i^*(r,j)=argmax_{i^\prime\in R(r,j)}x_i^\prime\),\(R(r,j)\)是输入子窗口的索引集。一个\(x_i\)可能对应着多个不同的输出\(y_{rj}\)。其后向传播形式为:
\[ \frac{\partial{L}}{\partial{x_i}} = \sum_r\sum_j[i=i^*(r,j)]\frac{\partial{L}}{\partial{y_{rj}}} \]
\(RoI\)池化层反向传播中损失函数\(L\)对输入节点\(x_i\)的梯度为\(L\)对各个有可能的候选区域\(r\)(\(x_i\)被第\(r\)个候选区域的第\(j\)个输出选为最大值)输出\(y_{rj}\)梯度的累加,上式中的判决函数具体如下:
\[ [i=i^*(r,j)] = \begin{cases} 1, & i=i^*(r,j) \ge 1 \\ 0, & \text{otherwise} \end{cases} \]
对于整个图像的分类,全连接层计算所消耗的时间是要小于卷积层的,但在这个模型中,有大量的\(RoI\)用于目标检测,所以全连接层的计算时间大概占用了整体模型的\(50\%\)。所以作者将大型的全连接层进行了\(SVD\)截断操作。一个全连接层可以参数化为\(u \times v\)大小的权重矩阵\(W\),对该矩阵用\(SVD\)转换可得:
\[ W \approx U\Sigma_tV^T \]
其中\(U\)为\(W\)的大小为\(u \times t\)的左奇异矩阵,\(\Sigma_t\)为\(W\)的大小\(t \times t\)的奇异值对角阵,\(V\)为\(W\)的大小\(v \times t\)的右奇异矩阵。经过这一个简单的压缩操作能得到一个很好的速度提升。
说说模型
作者在论文后面还以提问的形式对模型进行了一些讨论。首先是多项任务损失,它避免了去设计一个管道式的序列训练模型,实验结果也显示这种设计效果优于多阶段的训练。\(Fast \ RCNN\)模型还将\(RCNN\)模型的\(SVM\)换成了\(softmax\)层,\(softmax\)层在为\(RoI\)预测分数时引入了类之间的竞争,所以最终效果要优于\(SVM\)。最后有一个注意点,并不是候选框越多,模型的性能越好,作者实验发现稀疏的对象候选框能够提升模型的性能。
致谢
本文参考以下论文: