首先必须祝贺中华人民共和国成立70周年,为了庆祝国庆假期的到来,我抽空过了一遍SSD目标检测模型,然后趁热打铁更了博客。。。SSD算法跟以往的RCNN系列算法最大的区别就是它是单级式的,而RCNN系列是多级式的。具体的细节见下文。
基本框架
先前的RCNN系列算法基本上都遵循生成候选框、提取特征、分类和回归这一模式,而SSD以及类似算法采用的是在特征图上进行密集采样得到先验框再进行分类和回归。简单来讲,多级式和单极式的区分就是看有没有生成候选框这一过程。多级式含有这一过程,所以相关的算法检测速度较缓慢,但精度高;单级式算法没有这一过程,相关算法检测速度快但精度低。
\(SSD\)算法是基于前向传播的卷积算法生成固定尺寸的边界框以及框内存在的目标的得分再接一个非极大值抑制来生成最终的检测结果的。这里前半部分采用的卷积网络是用于图像分类的标准结构网络(再分类层之前进行截断),作者称之为\(base \ network\)。在\(base \ network\)后面接一些辅助结构便形成了\(SSD\)目标检测网络。这个模型有一些关键特征,列举如下。
Multi-scale feature maps for detection
作者在截断的基础网络后面接了一些卷积特征层,这些特征层的尺度逐渐递减。\(SSD\)模型会提取多个不同尺寸的卷积层的特征来进行目标检测,这就形成了多尺度特征图检测,大尺度特征可以用来检测小物体,小尺度特征用来检测大物体。这里作者还跟\(YOLO\)模型进行了比较,\(YOLO\)是在单一尺度的特征图上进行操作的,很明显这样获取的信息量要少于\(SSD\)的多尺度范围的检测,所以在精度方面\(SSD\)要优于\(YOLO\)。
Convolutional predictors for detection
在上面提到的添加卷积特征层中,每一层都可以使用一系列卷积来生成一系列固定大小的检测预测结果(这些预测要么是目标类别的得分,要么是边界框的偏置)。这一点跟\(YOLO\)算法不同,\(YOLO\)经过卷积层后还要经过全连接层再进行检测,而\(SSD\)直接采用卷积对不同的特征图进行提取检测结果。对于\(m \times n\)大小,通道数为\(p\)的卷积特征层,后接的检测卷积层基本的尺寸为\(3 \times 3 \times p\),即用小型核来进一步提取特征。输出的边界框偏置量是相对于先验框测量的,而先验框又是相对于每一个特征图的位置的。
Default boxes and aspect ratios
作者在每一张特征图上关联了一系列不同尺寸和长宽比的先验框,这类似于\(Faster \ RCNN\)的\(Anchor \ box\)。每一个先验框都会得到类别分数及其对应的边界框参数。对于特征图上的每个点都有\(k\)个先验框的情况,模型会计算对应于\(c\)个类别的置信度(这里注意\(SSD\)将背景也当为一个类而算进类别个数里面),\(4\)个偏置量。
注意:预测过程中,置信度最高的那个类别就是边界框所属的类别,而当第一个置信度最高时,则表示边界框中不包含目标。
这意味着会有\((c+4)k\)个卷积核应用于特征图上的各个位置,而对于\(m \times n\)大小的特征图,一共生成\((c+4)kmn\)个输出。这种方式跟\(Faster \ RCNN\)的\(anchor \ boxes\)很类似,但不同的是\(SSD\)将先验框应用于几个不同分辨率的特征图上,这种处理方式允许我们高效地离散化可能的输出框大小空间。
总体结构图如下:
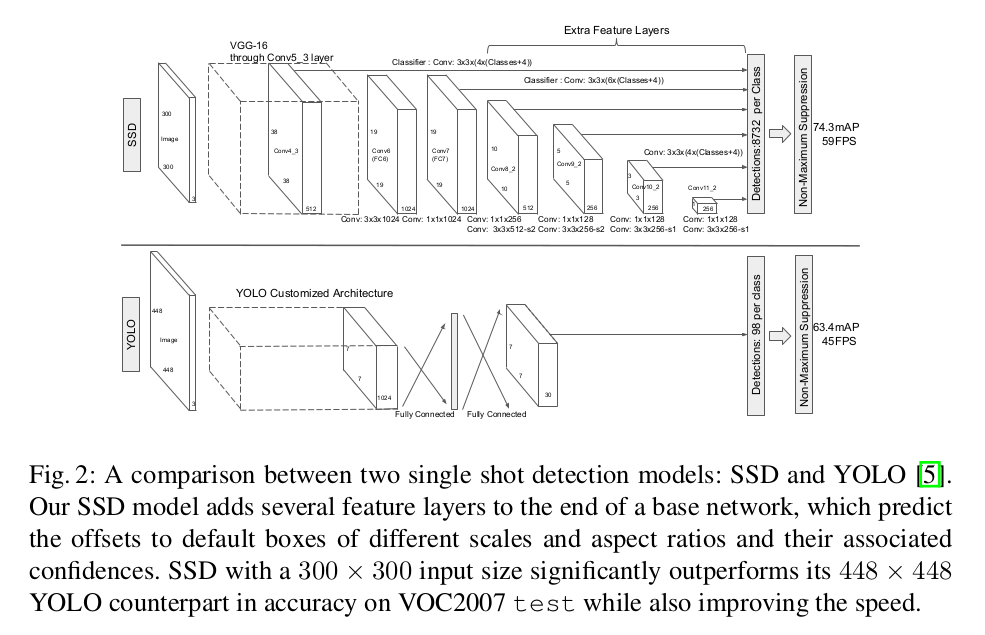
先验框的细节如下图:
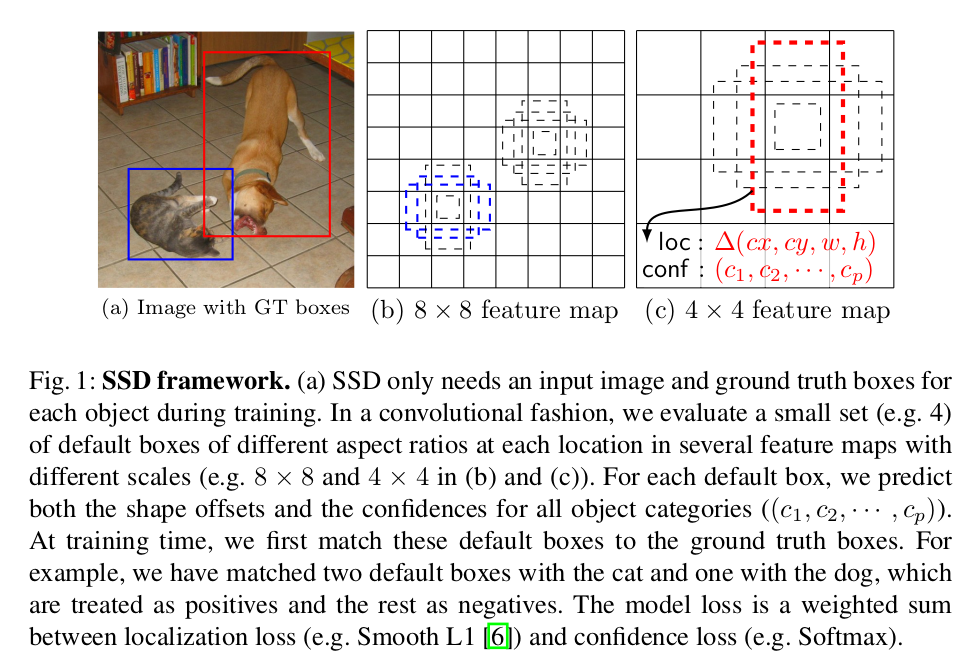
模型训练
\(SSD\)模型的训练与其它带有区域候选框的典型检测器不同,主要是\(SSD\)需要将真实实例信息分配给检测器输出的固定集合中的特定输出(这里附上作者原话:The key difference between training SSD and training a typical detector that uses region proposals, is that ground truth information needs to be assigned to specific outputs in the fixed set of detector outputs)。
在训练过程中,\(SSD\)需要确定哪个先验框对应哪个真实实例,并依据这些映射进行模型的训练。根据论文,先验框与\(ground \ truth\)的匹配原则如下:
- 对于图片中每个\(ground \ truth\),找到与其\(IoU\)最大的先验框,该框与其匹配,这样可以保证每个\(ground \ truth\)一定与某个先验框匹配;
- 剩余的未匹配先验框,若某个\(ground \ truth\)的\(IoU\)大于事先定下的阈值,则该先验框也与这个\(ground \ truth\)匹配。
上面的匹配原则会造成一个\(ground \ truth\)与多个先验框匹配,但不允许有一个先验框对应多个\(ground \ truth\)。
\(SSD\)训练的目标函数是来自于\(MultiBox\)的,但作者进行了扩展以处理多目标分类问题。定义\(x^P_{ij} \in \\{1,0\\}\)为指示函数,当\(x^P_{ij}=1\)时表示第\(i\)个先验框与第\(j\)个\(ground \ truth\)匹配并且\(ground \ truth\)的类别为\(P\)。在上面的匹配策略中,我们可以有\(\sum_ix^P_{ij} \ge 1\)。总体的损失函数是位置损失和置信度损失的加权和,如下:
\[ L(x,c,l,g) = \frac{1}{N}(L_{conf}(x,c)+\alpha L_{loc}(x,l,g)) \]
其中\(N\)表示先验框的正样本数,\(c\)为类别置信度预测值,\(l\)为先验框所对应边界框的位置预测值,\(g\)是\(ground \ truth\)的位置参数。位置损失采用的是\(Smooth \ L1 \ loss\),与\(Faster \ RCNN\)类似,作者对先验框中心\(d(cx,cy)\)及其宽度\(w\)和高度\(h\)的偏移量进行回归。这里注意要先对\(ground \ truth\)的\(g\)进行编码,因为预测值\(l\)为编码值。
\[ \begin{aligned} L_{loc}(x,l,g) & = \sum_{i\in Pos}^N \sum_{m\in \{cx,cy,w,h\}}x_{ij}^ksmooth_{L1}(l_i^m-\hat{g}_j^m) \\ \hat{g}_j^{cx} & = (g_j^{cx}-d_i^{cx})/d_i^w \\ \hat{g}_j^{cy} & = (g_j^{cy}-d_i^{cy})/d_i^h \\ \hat{g}_j^{w} & = log(\frac{g_j^w}{d_i^w}) \\ \hat{g}_j^{h} & = log(\frac{g_j^h}{d_i^h}) \\ \end{aligned} \]
置信度损失采用的是\(softmax \ loss\)。
\[ L_{conf}(x,c) = - \sum_{i \in Pos}^Nx_{ij}^Plog(\hat{c}_i^P)-\sum_{i \in Neg}log(\hat{c}_i^0) \]
其中
\[ \hat{c}_i^P = \frac{exp(c_i^P)}{\sum_Pexp(c_i^P)} \]
为了处理不同对象的尺寸不同问题,有些方法建议将图像处理成不同的尺寸然后再合并结果,这可以通过利用单个网络中几个不同层的特征图进行预测来得到相似的效果,而且还可以在所有对象比例尺上共享参数。在此前已经有实验验证了低层卷积层产生的低级特征图能有效地提升语义分割的效果,因为低级网络层捕捉到了更多的输入对象的细节。作者在\(SSD\)中同时使用了低层和高层的网络层进行目标检测。
从不同网络层获取的特征图会有不同的尺寸,而在\(SSD\)网络中,先验框不必需要去对应每一个网络层的实际感受野,作者设计了先验框的拼贴以便特定的特征图能对特定尺寸的对象做出响应。假设使用\(m\)个特征图来预测,每一个特征图上的先验框大小用下式计算:
\[ s_k = s_{min}+\frac{s_{max}-s_{min}}{m-1}(k-1), \ k \in [1,m] \]
这里设置\(s_{min}=0.2\)以及\(s_{max}=0.9\),表示最小尺寸为0.2,最大尺寸为0.9。先验框的尺度遵守一个线性递增规则:随着特征图大小的降低,先验框尺度线性增加。上式的\(s_k\)表示先验框相对于图片的比例。作者在先验框上强加了不同的长宽比,表示为\(a_r \in \\{1,2,3,\frac{1}{2},\frac{1}{3}\\}\),并利用下式计算先验框的长宽大小。
\[ \begin{aligned} w_k^a &= s_k\sqrt{a_r} \\ h_k^a &= s_k/\sqrt{a_r} \end{aligned} \]
对于长宽比为1的情况,作者添加了一个先验框(尺度为\(s_k^*=\sqrt{s_k s_{k+1}}\)),所以最终特征图每个位置会产生6个先验框。作者将先验框的中心坐标设置为\((\frac{i+0.5}{\vert f_k \vert},\frac{j+0.5}{\vert f_k \vert})\),这里\(\vert f_k \vert\)表示第k个特征图的大小并且\(i,j \in [0,\vert f_k \vert]\)。实际上,我们可以通过设计先验框的分布以适应特定的数据集。通过结合从多个特征图不同尺寸和长宽比生成的先验框完全可以布满整个图像,所以\(SSD\)可以算是密集采样。生成的先验框中有许多是负样本,这说明进行正负样本平衡是有必要的。作者采用了难分样本挖掘进行平衡,根据损失置信度对先验框进行排序,选择靠前的先验框并保持正负样本比例为\(1:3\)。
在数据增强方面,作者对训练中每一张图像从下面随机选择一项进行增强:
- 使用原始的全部图像;
- 采样块域以使与目标对象的最小\(jaccard \ overlap\)为0.1,0.3,0.5,0.7或0.9;
- 随机采样块域
其中每一个块域的大小为\([0.1,1]\)倍于原始图像大小,同时长宽比介于0.5和2之间。\(jaccard \ overlap\)(交并比,即为IOU)的计算如下:
\[ \begin{aligned} J(A,B) & = \frac{\vert A\cap B\vert}{\vert A\cup B\vert} \\ & = \frac{\vert A\cap B\vert}{\vert A \vert +\vert B\vert - \vert A\cap B\vert} \end{aligned} \]
这里有个注意点。在\(base \ network\)中,作者采用的是在\(ILSVRC \ CLS-LOC\)上进行过预训练的\(VGG16\)模型,将\(fc6\)和\(fc7\)转为卷积层,将池化层\(pool5\)由原来的\(stride=2\)的\(2\times 2\)转为\(stride=1\)的\(3\times 3\)。这里作者使用了\(Atrous\)算法来让模型适应这种变化(实际上是\(conv6\)层采用扩展卷积或带孔卷积在不增加模型参数和复杂度的情况下扩大感受野)。
其它模型上的细节可以参考原论文。
附言
在实现这个模型的过程中,minsize和maxsize这两个参数让我比较困扰(这两个参数用于生成每个特征层地先验框尺寸)。对比了其他一些源码后,大概的计算过程如下:
理论上,应该按原论文里给的公式进行计算:
\[ s_k = s_{min}+\frac{s_{max}-s_{min}}{m-1}(k-1), \ k \in [1.m] \]
其中\(s_k\)为每个特征层的先验框大小与原图大小之比,\(S_{min}\)和\(S_{max}\)分别表示最小、最大比例,这里依据论文设定\(S_{min} = 0.2\),\(S_{max} = 0.9\),\(m\)表示特征层个数(这里经过多份代码的对比,选用的m不是6而是5),\(k\)为第几个特征层。
而在实际使用中,我们需要考虑到取整的问题,所以使用的公式如下(这里选用向上取整,也可采用其它取整方式):
\[ s_k = \lceil{s_{min} \times 100}\rceil+\left\lceil{\frac{\lceil{s_{max}\times 100}\rceil-\lceil{s_{min}\times 100}\rceil}{m-1}}\right\rceil(k-1), \ k \in [1,m] \]
这样可以得到一系列数字:
\[ s1 \sim s6: 20, 38, 56, 74, 92, 110 \]
将其除以100转为真实比例:
\[ s1 \sim s6: 0.20, 0.38, 0.56, 0.74, 0.92, 1.10 \]
最后乘上原始图片的尺寸(这里选用的是300):
\[ 60, 114, 168, 222, 276, 330 \]
针对\(s1\),还有一个\(s1^{\prime}= 0.5\times s1\),最后可得:
\[ 30, 60, 114, 168, 222, 276, 330 \]
这样可以得到7个数值,对应6组\(minsize\)和\(maxsize\),由此可以计算出每一个特征层的先验框尺寸。
致谢
本文参考自: