IoU是目标检测里的一个重要指标,它是通过计算预测框与真实框的交集和并集的比值来衡量预测框的优劣。但通常的预测框调整函数一般采用的是L2范数,即以MSE的方式来计算损失,而目前来看,一些研究表明这并非最优的优化函数,所以就有了IOU损失函数。
IoU的计算:
\[ IoU = \frac{\vert B \cap B^{gt}\vert}{\vert B \cup B^{gt}\vert} \]
其中\(B\)表示的是预测框,\(B^{gt}\)表示的是真实框,整体上看\(IoU\)就是预测框与真实框的交集与预测框与真实框的并集的比值。它可以有效的反映出预测框的检测效果,同时它还具有尺度不变性,即对尺度不敏感。
IoU Loss
从\(IoU\)的计算公式可以简单粗暴的得到一个损失函数:
\[ \mathcal{L}_{IoU} = 1-IoU = 1-\frac{\vert B \cap B^{gt}\vert}{\vert B \cup B^{gt}\vert} \]
这个损失函数有一个不可避免的缺陷:当两个框无交集时,损失恒为1,这样距离小的无交集和距离远的无交集的输出是一样的,失去了梯度的方向,无法优化。
Note: \(Iou \ Loss\)的实现形式不止上面提到的那种,例如还有\(UnitBox\)的交叉熵形式和\(IoUNet\)的\(Smooth-L1\)的形式,但都有上述问题。
GIoU Loss(generalized IoU loss)
为了解决上述问题,\(GIoU\)出现了。它在\(IoU \ loss\)的基础上添加了一个惩罚项。当预测框与真实框的距离越大时,惩罚项的值越大。具体公式如下:
\[ \mathcal{L}_{GIoU} = 1-IoU+\frac{\vert C-B\cup B^{gt}\vert}{\vert C\vert} \]
其中\(C\)是包含预测框和真实框的最小包围框。在训练过程中,\(GIoU \ loss\)倾向于先增大预测框使其与真实框有重合,然后在公式中的\(IoU\)项的引导下来最大化重叠区域。但当真实框完全包含预测框时,上述公式中的惩罚项则为0,即\(GIoU loss\)降级为\(IoU \ loss\),同时由于该损失过分依赖于\(IoU\)项,需要跟多的迭代次数来收敛,特别时水平和垂直方向。
DIoU Loss(Distance-IoU loss)
与\(GIoU\)相同的是,\(DIoU\)也是在\(IoU \ loss\)的基础上添加一个惩罚项,但\(DIou\)考虑了预测框与真实框的距离、重叠率以及尺度,具体如下:
\[ \begin{aligned} \mathcal{L}_{DIoU} & = 1-IoU+\mathcal{R}(\mathcal{B}, \mathcal{B}^{gt}) \\ \mathcal{R}_{DIoU} & = \frac{\rho^2(b, b^{gt})}{c^2} \end{aligned} \]
其中,\(b\)和\(b^{gt}\)分别表示预测框和真实框的中心点,\(\rho\)代表的是计算两点的距离公式,在这里为两个中心点的欧式距离,\(c\)代表的是包含预测款和真实框的最小框的对角线距离,详细如下图所示。
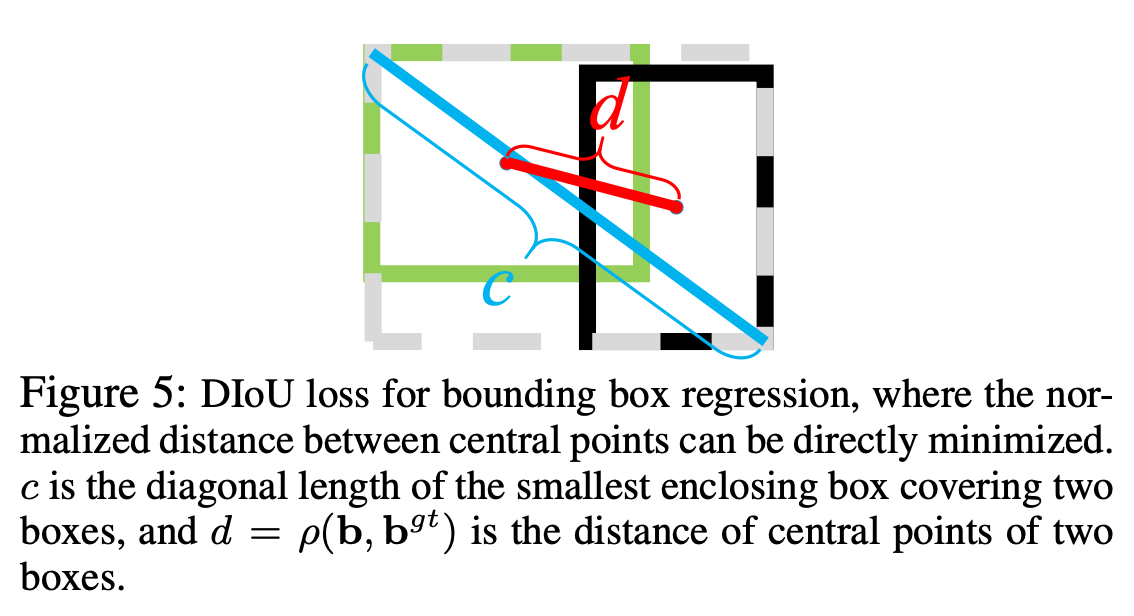
该损失函数直接最小化两个框的距离,所以收敛速度要快于\(GIoU\)。\(DIoU\)可以应用于\(NMS\),使得到的框更加合理。
CIoU(Complete IoU Loss)
在\(DIoU\)的基础上考虑框的长宽比的话即可得到\(CIoU\),具体如下:
\[ \begin{aligned} \mathcal{L}_{CIoU} & = 1-IoU+\mathcal{R}(\mathcal{B}, \mathcal{B}^{gt}) \\ \mathcal{R}_{CIoU} & = \frac{\rho^2(b, b^{gt})}{c^2}+\alpha \mathcal{v} \\ \mathcal{v} & = \frac{4}{\pi^2}\left(arctan\frac{\mathcal{w}^{gt}}{\mathcal{h}^{gt}}-arctan\frac{\mathcal{w}}{\mathcal{h}}\right)^2 \\ \alpha & = \frac{\mathcal{v}}{(1-IoU)+\mathcal{v}} \end{aligned} \]
Note:
\(CIoU\)的梯度中包含有\(\mathcal{v}\)的梯度,其梯度大致如下:
\[ \begin{aligned} \frac{\partial\mathcal{v}}{\partial\mathcal{w}} & = \frac{8}{\pi^2}\left(arctan\frac{\mathcal{w}^{gt}}{\mathcal{h}^{gt}}-arctan\frac{\mathcal{w}}{\mathcal{h}}\right)\times\frac{\mathcal{h}}{\mathcal{w}^2+\mathcal{h}^2} \\ \frac{\partial\mathcal{v}}{\partial\mathcal{h}} & = -\frac{8}{\pi^2}\left(arctan\frac{\mathcal{w}^{gt}}{\mathcal{h}^{gt}}-arctan\frac{\mathcal{w}}{\mathcal{h}}\right)\times\frac{w}{\mathcal{w}^2+\mathcal{h}^2} \end{aligned} \]
在长宽比在\([0,1]\)的情况下,\(\mathcal{w}^2+\mathcal{h}^2\)的值通常会很小,\(\frac{1}{\mathcal{w}^2+\mathcal{h}^2}\)的值会比较大可能会导致梯度爆炸,所以实现中一般将其替换为常数1。
致谢
本文参考以下内容:
Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression