通常的目标检测算法都是基于Anchor来做的,这样虽然会生成许多无用的锚框,同时带来耗时的NMS后处理操作,但算法的准确率较高,因为锚框基本上覆盖来所有目标区域。在检测领域还有一种做法的基于Anchor free的,即无锚框,我了解的范围内主要有Cornernet、Centernet(Keypoint Triplets for Object Detection)和Centernet(Objects as Points)。这种类型的算法无需生成锚框,也就不需要耗时的NMS后处理。这里主要记录一下Centernet(Objects as Points)的处理方法。
模型结构
Centernet主要是借用关键点检测的操作来检测目标的中心位置,再扩展到目标检测领域上,即通过回归得到框的大小。该算法可以方便地扩展到其它领域,例如论文里提到的目标检测、3D框预测、姿态等。在backbone方面作者主要采用了hourglass、resnet和DLA模型,对于目标检测,则在backbone后面加上三个分支,主要是:Heat maps分支用于获取目标中心点、Center offset用于矫正目标中心点、Box size用于回归目标框大小。大致结构如下(其中的cls表示检测的类别数):
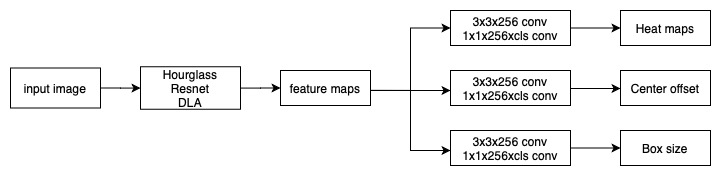
数据流
说完模型结构,接下来是对数据的处理。作者是通过热图来标注目标中心点的,而热图是由高斯核得到的。
首先对图片\(H\times W\times 3\)经过下采样处理(下采样倍数\(R\)这里设置为\(4\))得到\(H/R\times W/R\times cls\)的图像,其中\(cls\)为类别数。之后计算真实框在缩放后图像上的中心点\(\hat{p}(x,y)=\lfloor\frac{p}{R}\rfloor\),通过高斯核\(exp(-\frac{(x-\hat{p}_x)^2+(y-\hat{p}_y)^2}{2\sigma_p^2})\)对中心点进行映射,最后得到热图\(\hat{Y}\in [0,1]^{\frac{W}{R}\times\frac{H}{R}\times 3}\)。
生成的热图并非是中心点位置为1,其它位置为0。它是目标点为1,向周围扩散逐渐变小。高斯核映射中以\(\hat{p}\)为中心画出对应的高斯函数,并截取以\(\hat{p}\)为圆心,\(radius\)为半径的区域,同时高斯核中的\(\sigma_p\)为目标尺寸自适应标准差,作者实现中将其赋值为\(\frac{2\times radius}{6}\)。这里截取区域半径\(radius\)以及高斯核参数\(\sigma_p\)的设计均参考了另一篇论文Cornernet。在Cornernet中,高斯核的标准差差设计为偏差允许区域半径(即\(radius\))的\(\frac{1}{3}\)。考虑到在目标点(Cornernet的目标点为目标框的角点)附近的点生成的标记框与目标框会有较大的IoU,直接将该点赋值为0并不合适,所以通过设置IoU阈值(Centernet中设置为0.7)形成偏差允许区域,在该区域内按照高斯函数来逐渐递减目标点周围点的数值。由这些点生成的标记框与目标框有三种相交极限情况,分别计算这三种情况下的区域半径取值,最后取三种情况下的最小区域半径即为\(radius\)的值。
radius的计算
标记框全外切目标框
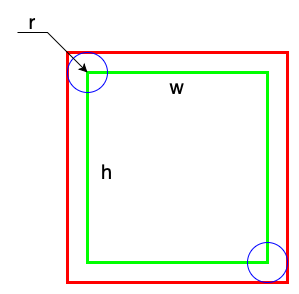
由上图可计算出IoU:
\[ IoU = \frac{w\cdot h}{(w+2r)\cdot(h+2r)} \ge iou\_overlap \]
则该情况下的最大半径满足下式:
\[ \begin{aligned} & \frac{w\cdot h}{(w+2r)\cdot(h+2r)} = k = iou\_overlap \\ \Rightarrow & \ 4k\cdot r^2 + 2k(w+h)\cdot r + (k-1)wh = 0 \end{aligned} \]
这是一个一元二次方程,在保证有解的情况下,可由公式计算出\(r\)的正解。(\(y = \frac{-b\pm\sqrt{b^2-4ac}}{2a}\),其中\(b^2-4ac\ge 0\))。
标记框全内切目标框
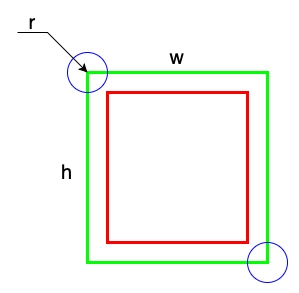
由上图可计算出IoU:
\[ IoU = \frac{(w-2r)\cdot(h-2r)}{w\cdot h} \ge iou\_overlap \]
则该情况下的最大半径满足下式:
\[ \begin{aligned} & \frac{(w-2r)\cdot(h-2r)}{w\cdot h} = k =iou\_overlap \\ \Rightarrow & \ 4\cdot r^2 - 2(w+h)\cdot h + (1-k)wh = 0 \end{aligned} \]
同样可以求取\(r\)的正解
标记框半外切半内切目标款
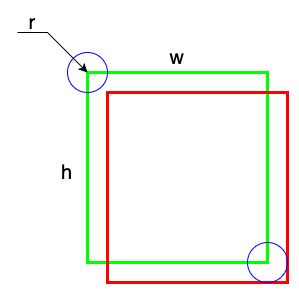
可计算IoU如下:
\[ IoU = \frac{(w-r)\cdot(h-r)}{2\cdot h\cdot w - (w-r)\cdot(h-r)} \ge iou\_overlap \]
则该情况下的最大半径满足下式:
\[ \begin{aligned} & \frac{(w-r)\cdot(h-r)}{2\cdot h\cdot w - (w-r)\cdot(h-r)} = k = iou\_overlap \\ \Rightarrow & \ (1+k)\cdot r^2 - (w+h)(1+k)\cdot r + (1-k)wh = 0 \\ \Rightarrow & \ r^2 -(w+h)\cdot r + \frac{1-k}{1+k}wh = 0 \end{aligned} \]
同理可以求出\(r\)的正解
综合以上三种情况,取三者中的最小值作为\(radius\)的取值。
损失函数
该模型具有良好的可扩展性,通过添加不同的分支可以应用于不同的领域,其中有两个分支是固定的(Heat maps和Center offset),对应的损失函数分别为中心点损失和中心点偏差损失。
中心点损失
作者这里也是借鉴了Cornernet的损失函数来设计的,形式如下:
\[ L_k = -\frac{1}{N} \begin{cases} (1-\hat{Y}_{xyc})^\alpha log(\hat{Y}_{xyc}) \ & \text{if } Y_{xyc}=1 \\ (1-Y_{xyc})^\beta(\hat{Y}_{xyc})^\alpha log(1-\hat{Y}_{xyc}) \ & \text{otherwise} \end{cases} \]
其中\(N\)表示图片中目标中心点的个数,\(\alpha\)和\(\beta\)为超参数,作者选用了\(\alpha=2\)和\(\beta=4\)。\(Y_{xyc}\)表示真实标注热图上对应位置的取值,而\(\hat{Y}_{xyc}\)表示模型预测的热图上对应位置的取值。
从整体上看,这是一个改进后的\(focal \ loss\)函数。当\(Y_{xyc}=1\)时,可以通过\((1-\hat{Y}_{xyc})^\alpha\)来改变对应的权重,若模型预测值已经接近\(1\),表明该样本对于模型来说属于容易样本,则对应的损失权重会降低,反之属于困难样本,权重上升。
当\(Y_{xyc}\neq 1\)时,这里可以分为两种情况,一种是预测点离目标点较近即\(1-Y_{xyc}\)较小,此时模型预测值应该为0,若模型预测值接近1,对应样本损失的权重上升,但该点离目标点较近,模型在该点取得的预测值较大是可以接受的,所以用\((1-Y_{xyc})^\beta\)来下降权重进行平衡;另一种是预测点离目标点较远,即\(1-Y_{xyc}\)较大,在\((1-Y_{xyc})^\beta\)的作用下,对应样本损失的权重会增大,但该点离目标点较远,模型在该点取得的预测值较小是可以接受的,所以用\(\hat{Y}_{xyc}^\alpha\)来降低权重进行平衡。
中心点偏差损失
由于在对真实标注进行下采样时对中心点坐标做了取舍,引入了偏差,所以使用L1损失来引导模型弥补这段差值:
\[ \begin{aligned} L_{off} &= \frac{1}{N}\sum_p\lvert \hat{O}_{\hat{p}} - (\frac{p}{R}-\hat{p})\rvert \\ &= \frac{1}{N}\sum_p\lvert \hat{O}_{\hat{p}} - (\frac{p}{R}-\lfloor \frac{p}{R}\rfloor)\rvert) \end{aligned} \]
其中\(N\)表示图片中目标中心点的个数,\(\hat{O}\in \mathcal{R}^{\frac{W}{R}\times\frac{H}{R}\times 2}\)表示模型预测的中心点偏差。注意该损失函数仅在对应的目标点上起作用,其余位置均忽略。
其它损失
模型可以进行扩展,对应的损失函数也不太一样,这里只说明一下目标检测下的损失函数。
令\((x_1^{(k)}, y_1^{(k)}, x_2^{(k)}, y_2^{(k)})\)表示类别\(c_k\)中目标\(k\)的目标框坐标,其中心点坐标为\(p_k=(\frac{x_1^{(k)}+x_2^{(k)}}{2}, \frac{y_1^{(k)}+y_2^{(k)}}{2})\),对于目标检测,模型主要回归每个目标框的尺寸\(s_k=(x_2^{(k)}-x_1^{(k)}, y_2^{(k)}-y_1^{(k)})\)。为了减轻计算负担,作者对每个类别对象使用了统一的目标框尺寸,即每个类别下的所有目标只有一个尺寸大小。使用L1损失如下:
\[ L_{size} = \frac{1}{N}\sum_{k=1}^N\lvert \hat{S}_{p_k} - s_k\rvert \]
其中\(N\)表示图片中目标中心点的个数,\(\hat{S}\in \mathcal{R}^{\frac{W}{R}\times \frac{H}{R}\times 2}\)表示模型预测的目标框尺寸。
作者并没有对尺寸进行归一化,而是通过添加系数来缩放损失大小:
\[ L_{det} = L_k + \lambda_{size}L_{size} + \lambda_{off}L_{off} \]
上式是针对于目标检测的,作者选取的两个超参数值为\(\lambda_{size}=0.1\)和\(\lambda_{off}=1\)。
推断阶段
在模型的热图输出上,对每个类别都提取出\(topK\)个高峰。提取的点是在该点在周围8个点内为最大,这步操作可通过一个\(3\times 3\)的最大池化来完成。这里其实相当于进行NMS。之后通过获取的峰值点、中心点偏差预测值以及预测尺寸即可得到相应的预测框:
\[ \begin{aligned} &(\hat{x}_i+\delta\hat{x}_i-\hat{w}_i/2,\ \hat{y}_i+\delta\hat{y}_i-\hat{h}_i/2\\ &\hat{x}_i+\delta\hat{x}_i+\hat{w}_i/2,\ \hat{y}_i+\delta\hat{y}_i+\hat{h}_i/2) \end{aligned} \]