数学是科学之王。 ——高斯
概率无向图模型
在了解概率无向图模型之前,先看看概率图模型(PGM,probabilistic graphical model)的定义:它是由图表示的概率分布。设有联合概率分布\(P(Y)\),\(Y\in \mathcal{Y}\)是一组随机变量,由无向图\(G=(V, E)\)表示概率分布\(P(Y)\),即在图\(G\)中,结点\(v\in V\)表示一个随机变量\(Y_v\),\(Y_v=(Y_v)_{v\in V}\);边\(e\in E\)表示随机变量之间的概率依赖关系。
给定一个概率联合分布\(P(Y)\)和表示它的无向图\(G\)。以下说明三个性质。
成对马尔可夫性(pairwise Markov property)
\[ P(Y_u,Y_v\mid Y_O) = P(Y_u\mid Y_O)P(Y_v\mid Y_O) \]
其中\(u\),\(v\)为无向图中任意两个没有边连接的结点,对应的随机变量分别为\(Y_u\)和\(Y_v\),\(O\)为无向图中除了\(u\)、\(v\)外的其他所有结点,对应的随机变量组为\(Y_O\)。即给定随机变量组为\(Y_O\)的条件下,随机变量\(Y_u\)和\(Y_v\)是条件独立的。
局部马尔可夫性(local Markov property)
\[ P(Y_u,Y_O\mid Y_W) = P(Y_v\mid Y_W)P(Y_O\mid Y_W) \]
其中\(v\in V\)为无向图\(G\)中任意一个结点,对应的随机变量为\(Y_v\),\(W\)是与\(v\)有边连接的所有结点,对应随机变量组为\(Y_W\),\(O\)是\(v\),\(W\)之外的其他所有结点,对应随机变量组为\(Y_O\)。即给定随机变量组\(Y_W\)的条件下随机变量\(Y_v\)与随机变量组\(Y_O\)是独立的。
全局马尔可夫性(global Markov property)
\[ P(Y_A,Y_B\mid Y_C) = P(Y_A\mid Y_C)P(Y_B\mid Y_C) \]
其中结点集合\(A\)、\(B\)是在无向图\(G\)中被结点集合\(C\)分开的任意结点集合,对应的随机变量组分别为\(Y_A\),\(Y_B\),\(Y_C\)。即给定随机变量组\(Y_C\)条件下随机变量组\(Y_A\)和\(Y_B\)是条件独立的。
上述三种定义是等价的。
综合以上给出概率无向图模型的定义。设有联合概率分布\(P(Y)\),由无向图\(G=(V,E)\)表示,在图\(G\)中,结点表示随机变量,边表示随机变量之间的依赖关系,如果联合概率分布\(P(Y)\)满足成对、局部或全局马尔可夫性,就称此联合概率分布为概率无向图模型(probability undirected graphical model),或马尔可夫随机场(MRF,Markov random field)。
因子分解
概率图模型的核心是计算联合概率分布
无向图\(G\)中任何两个结点均有边连接的结点子集称为团(clique)。若\(C\)是无向图\(G\)的一个团,并且不能再加进任何一个\(G\)的结点使其成为一个更大的团,则称此\(C\)为最大团(maximal clique)。
将概率无向图模型的联合概率分布表示为其最大团上的随机变量的函数的乘积形式的操作为概率无向图模型的因子分解(factorization)。
给定概率无向图模型,设其无向图为\(G\),\(C\)为\(G\)上的最大团,\(Y_c\)表示\(C\)对应的随机变量。由Hammersley-Cliffoed定理有当且仅当随机变量的联合概率密度严格为正时,概率无向图模型等价于吉布斯随机场(GRF,Gibbs Random Field)。而GRF的联合概率分布\(P(Y)\)可写成图中所有最大团\(C\)上的函数\(\Psi_C(Y_C)\)的乘积形式,即:
\[ \begin{aligned} P(Y) & = \frac{1}{Z}\prod_C\Psi_C(Y_C) \\ Z & = \sum_Y\prod_C\Psi_C(Y_C) \end{aligned} \]
其中\(Z\)是规范化因子(normalization factor),用于保证\(P(Y)\)构成一个概率分布,即和为1。函数\(\Psi_C(Y_C)\)称为势函数(potential function)。这里要求势函数是严格为正的,为了方便,通常定义为指数函数:
\[ \Psi_C(Y_C) = exp\{-E(Y_C)\} \]
条件随机场
定义:设\(X\)与\(Y\)是随机变量,\(P(X\mid Y)\)是在给定\(X\)的条件下\(Y\)的条件概率分布,若随机变量\(Y\)构成一个由无向图\(G=(V,E)\)表示的马尔可夫随机场,即
\[ P(Y_v\mid X,Y_w,w\ne v) = P(Y_v\mid X,Y_w,w\sim v) \]
对任意结点\(v\)成立,则称\(P(Y\mid X)\)为条件随机场。其中\(w\sim v\)表示在图\(G=(V,E)\)中与结点\(v\)有边连接的所有结点\(w\),\(w\ne v\)表示结点\(v\)以外的所有结点,\(Y_v\)、\(Y_u\)与\(Y_w\)为结点\(v\),\(u\)与\(w\)对应的随机变量。
\(X\)、\(Y\)可以有不同的图结构,但一般情况下假设他们有相同的图结构,这就有线性条件随机场(linear chain conditional random field)。设\(X=(X_1,X_2,\cdots,X_n)\),\(Y=(Y_1,Y_2,\cdots,Y_n)\)均为线性链表示的随机变量序列,若在给定随机变量序列\(X\)的条件下,随机变量序列\(Y\)的条件概率分布\(P(Y\mid X)\)构成条件随机场,即满足马尔可夫性
\[ P(Y_i\mid X,Y_1,\cdots,Y_{i-1},Y_{i+1},\cdots,Y_n) = P(Y_i\mid X,Y_{i-1},Y_{i+1}) \\ i=1,2,\cdots,n \ (在i=1和n时只考虑单边) \]
则称\(P(Y\mid X)\)为线性链条件随机场,也是对数线性模型(log linear model)。
线性链条件随机场参数化形式
对于线性链条件随机场\(P(Y\mid X)\),在随机变量\(X\)取值为\(x\)的条件下,随机变量\(Y\)取值为\(y\)的条件概率有参数化形式如下:
\[ P(y\mid x) = \frac{1}{Z(x)}exp\left(\sum_{i,k}\lambda_kt_k(y_{i-1},y_i,x,i)+\sum_{i,l}\mu_ls_l(y_i,x,i)\right) \]
其中
\[ Z(x) = \sum_yexp\left(\sum_{i,k}\lambda_kt_k(y_{i-1},y_i,x,i)+\sum_{i,l}\mu_ls_l(y_i,x,i)\right) \]
式中,\(t_k\)和\(s_l\)是特征函数,\(\lambda_k\)和\(\mu_l\)是对应的权重,\(Z(x)\)是规范化因子,求和是在所有可能的输出序列上进行的。\(t_k\)是定义在边上的特征函数,为转移特征,依赖于当前和前一个位置,\(s_l\)是定义在结点\(l\)上的特征函数,为状态特征,依赖于当前位置,这两个特征函数都依赖于位置,是局部特征函数,而且一般取值为1或0,满足条件时为1否则为0。
线性链条件随机场简化形式
设转移特征有\(K_1\)个,状态特征有\(K_2\)个,且\(K=K_1+K_2\),有
\[ \begin{aligned} & f_k(y_{i-1},y_i,x,i) = \begin{cases} t_k(y_{i-1},y_i,x,i), &\ k=1,2,\cdots, K_1 \\ s_l(y_i,x,i), &\ k=K_1+l;\ l=1,2,\cdots, K_2 \end{cases} \\ & \Rightarrow f_k(y,x) = \sum_{i=1}^nf_k(y_{i-1},y_i,x,i), \qquad k=1,2,\cdots,K \end{aligned} \]
同样,用\(w_k\)来统一表达权值:
\[ w_k = \begin{cases} \lambda_k, &\ k=1,2,\cdots,K_1 \\ \mu_l, &\ k=K_1+l;\ l=1,2,\cdots,K \end{cases} \]
综上可得:
\[ P(y\mid x) = \frac{1}{Z(x)}exp\sum_{k=1}^{K}w_kf_k(y,x) \\ Z(x) = \sum_yexp\sum_{k=1}^Kw_kf_k(y,x) \]
若用\(w=(w_1,w_2,\cdots,w_K)^T\)表示权值向量,\(F(y,x)=(f_1(y,x),f_2(y,x),\cdots,f_K(y,x))^T\)表示全局特征向量,则上式可进一步表达如下:
\[ P_w(y\mid x) = \frac{exp(w\cdot F(y,x))}{Z_w(x)} \\ Z_w(x) = \sum_yexp(w\cdot F(y,x)) \]
线性链条件随机场矩阵形式
对于输入序列\(x\)的每个位置\(i=1,2,\cdots,n+1\),定义一个\(m\)阶矩阵(\(m\)是标记\(y_i\)取值的个数):
\[ M_i(x) = [M_i(y_{i-1},y_i\mid x)] \\ M_i(y_{i-1},y_i\mid x) = exp(W_i(y_{i-1},y_i\mid x)) \\ W_i(y_{i-1},y_i\mid x) = \sum_{k=1}^Kw_kf_k(y_{i-1},y_i,x,i) \]
由上面的简化形式结合这里的\(m\)阶矩阵有
\[ \begin{aligned} & exp\sum_{k=1}^Kw_k\sum_{i=1}^nf_k(y_{i-1},y_i,x,i) \\ = & exp\sum_{k=1}^K\sum_{i=1}^nw_kf_k(y_{i-1},y_i,x,i) \\ = & exp\sum_{i=1}^n\sum_{k=1}^Kw_kf_k(y_{i-1},y_i,x,i) \\ = & exp\sum_{i=1}^nW_i(y_{i-1},y_i\mid x) \\ = & \prod_{i=1}^nexp(W_i(y_{i-1},y_i\mid x)) \\ = & \prod_{i=1}^nM_i(y_{i-1},y_i\mid x) \\ = & \prod_{i=1}^{n+1}M_i(y_{i-1},y_i\mid x) \qquad (添加起点状态和终止状态) \end{aligned} \]
上面推导的最后一步中\(y_0=start\)和\(y_{n+1}=stop\)分别表示考试状态和终止状态。可得:
\[ P_w(y\mid x) = \frac{1}{Z(x)}\prod_{i=1}^{n+1}M_i(y_{i-1},y_i\mid x) \\ Z_w(x) = (M_1(x)M_2(x)\cdots M_{n+1}(x))_{start,stop} \]
规范化因子\(Z_w(x)\)是以start为起点stop为终点通过状态的所有路径\(y_1y_2\cdots y_n\)的非规范化概率\(\prod_{i=1}^{n+1}M_i(y_{i-1},y_i\mid x)\)之和。
一些应用
CRF适用于对上下文相关的样本间存在依赖关系的情况。在NLP领域有着大量的应用,对于CV领域,受限于本人的见识,目前见到的应用都是在图片分割领域。分割是像素级的,所以图像中的每一个像素都是一个结点\(x\),对应的标签即为\(y\),像素与像素之间的关系可以表示为边,由于周围像素对标签的影响程度要远大于其它像素,所以我们可以通过周围像素的标签来推断出目标像素的标签,这一套下来就形成了条件随机场。
DenseCRF
DenseCRF为全连接条件随机场,与普通条件随机场的不同就在于,二元势函数描述的是每一个像素与其他所有像素的关系。
由之前的定义可知,CRF的势函数为\(\Phi_c(X_c)=e^{-E(X_c)}\)(可选用其它函数,但需保证\(\Phi_c(X_c) > 0\)恒成立),其中\(E(X_c)\)为能量函数,对于分割领域,能量函数表达式一般如下:
\[ E(X) = \sum_i\phi_u(x_i)+\sum_{i<j}\phi_p(x_i,x_j) \]
其中第一项为一元势函数,用于衡量单一像素分类错误导致的能量增加情况。第二项为二元势函数,描述像素点与像素点之间的关系,鼓励相似像素分配相同的标签,而相差较大的像素分配不同标签,而这个“相似”的定义与颜色值和实际相对距离有关,表达式如下:
\[ \Phi_p(x_i,x_j) = \mu(x_i,x_j)\sum_{m=1}^Kw^{(m)}k^{(m)}(f_i,f_j) \]
其中\(\mu(x_i,x_j\)为label compatibility,它约束了像素之间的传导。只有相同标签的情况下,能量才可以传导。\(w^{(m)}\)为权值参数,\(k^{(m)}(f_i,f_j)\)为高斯核特征函数:
\[ k^{(m)}(f_i,f_j) = w^{(1)}exp\left(-\frac{\vert p_i-p_j\vert^2}{\theta_{\alpha}^2}-\frac{\vert I_i-I_j\vert^2}{2\theta_{\beta}^2}\right) + w^{(2)}exp\left(-\frac{\vert p_i-p_j\vert^2}{2\theta_{\gamma}^2} \right) \]
式中以特征的方式表示了不同像素之间的相似度,其中第一项为表面核(appearence kernel),主要是考虑到附近类似颜色的像素很可能属于同一类的事实,第二项为平滑核(smoothess kernel),主要用于消除一些小的独立像素区域(即噪声)。
一元势函数的输入为概率分布图,即由模型输出的特征图经过softmax函数运算得到的结果;二元势函数中的位置信息和颜色信息则由原始影像提供。
CRF通常是放置在卷积神经网络之后用于调整平滑网络的输出。一般来说,能量越大的物质存在的概率越小,能量越小的物质存在的概率越大。所以我们需要最小化这个能量函数\(E(X)\)就可以得到当前图片下最有可能的分割结果。这一步最小化操作为了节省计算量一般会通过平均场近似(Mean Field Approximation)来计算,即最小化近似分布与目标分布之间的KL散度,由于公式繁多,这里就不作推导,详情可以参考DenseCRF的论文补充材料。
CRFasRNN
上面的DenseCRF是作为后处理的方式添加在卷积模型后面的,而CRFasRNN是将CRF的迭代过程整合到卷积网络中形成一个end-to-end的模型。
论文与DenseCRF类似也使用来平均场近似来最小化能量函数,由于计算过程只设计到了加乘,所以可以利用类似卷积的结构将计算过程表达出来,并以此合并到卷积网络中,同时为了获得更精确的结果,作者还吧迭代过程也结合进去了,即在这一层“卷积层”中会进行迭代计算,类似与RNN的操作。
下图是平均场近似的迭代算法

将平均场近似计算中的步骤转换如下:
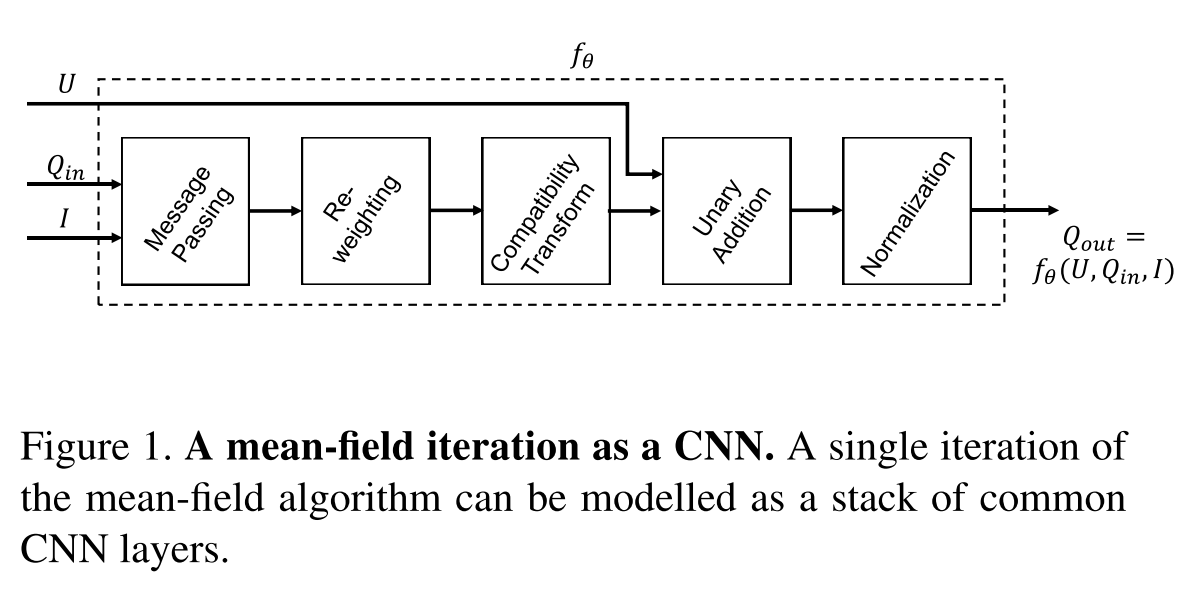
最后的CRFasRNN大致结构:
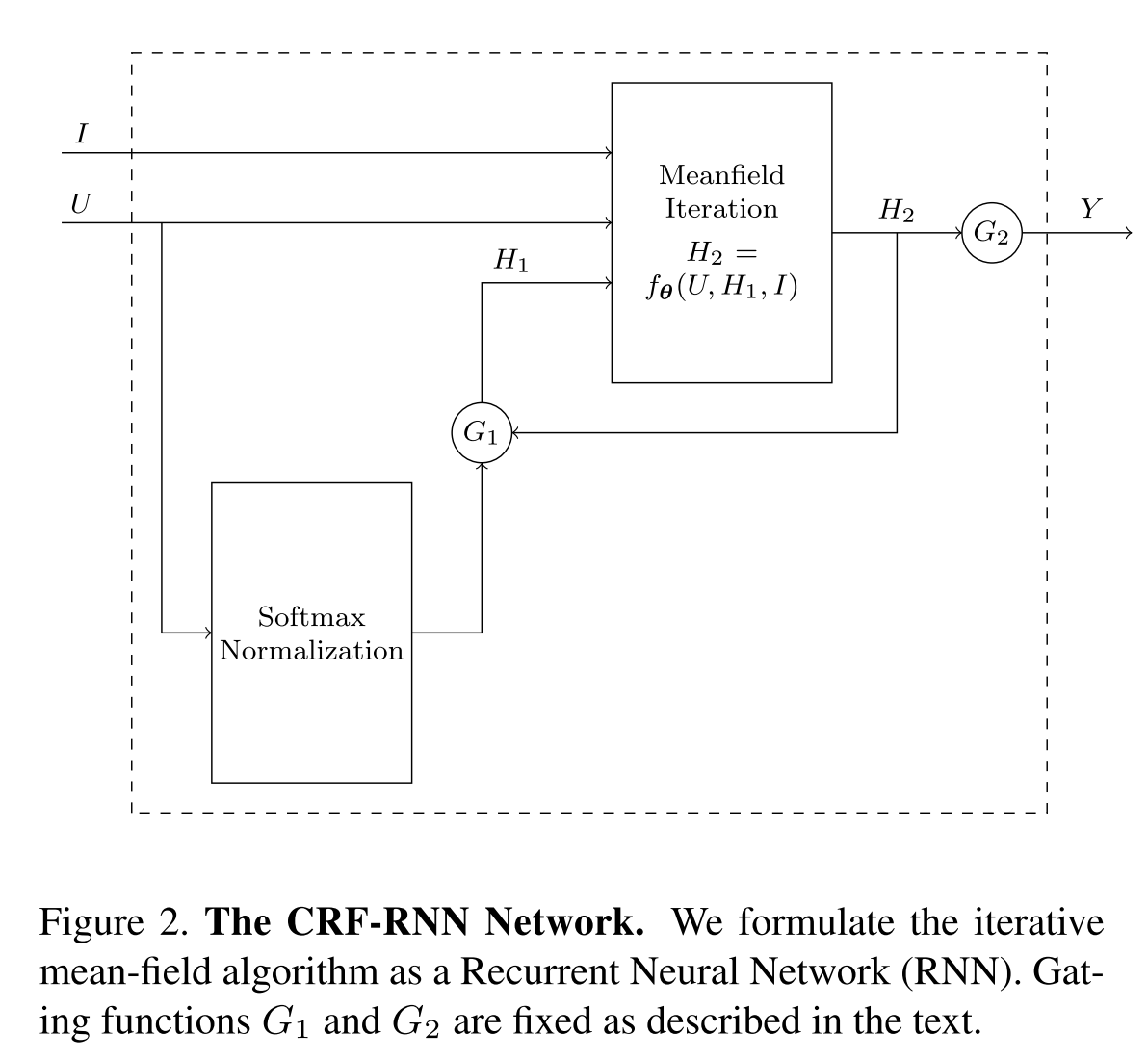

其中有
\[ \begin{aligned} H_1(t) & = \begin{cases} softmax(U), &\ t=0 \\ H_2(t-1), &\ 0<t\le T \end{cases} \\ H_2(t) & = f_{\theta}(U,H_1(t),I), \ 0\le t\le T \\ Y(t) & = \begin{cases} 0, &\ 0\le t<T \\ H_2(t), &\ t=T \end{cases} \end{aligned} \]
\(T\)为平均场计算的迭代次数,一般为10以内,论文设置为5。
以上就是我这段时间参考学习的条件随机场和一些应用,在图像分割上概率图模型的应用不止于此,还有好一些我后续再视情况更新。:>
致谢
统计学习方法 李航
Efficient Inference in Fully Connected CRFs with Gaussian Edge Potentials
Efficient Inference in Fully Connected CRFs with Gaussian Edge Potentials Supplementary Material