让它动起来。
Dynamic Convolution
一般的静态卷积用同一个卷积核对所有输入图像做相同的操作,而动态卷积会对不同的图像做调整,用更适合的卷积参数进行处理,这样可以在不增加网络深度或宽度的情况下增加模型的表达能力。
动态卷积根据注意力动态地聚合多个并行卷积核。注意力会根据输入动态地调整每个卷积核的权重,从而生成自适应的动态卷积。由于注意力是输入的函数,动态卷积不再是一个线性函数。通过注意力以非线性的方式叠加卷积核具有更强的表示能力。大致结构如下:
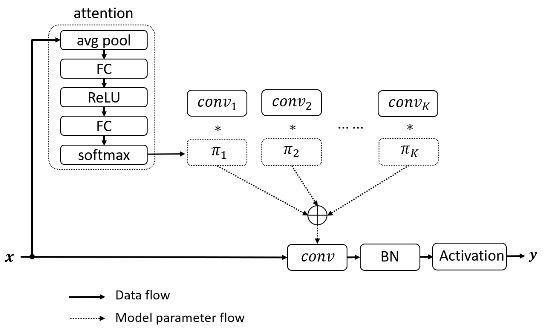
如上所示,动态卷积相比普通静态卷积引入了两部分额外的计算:注意力模块和卷积核的叠加。但这两部分的计算量很少,并且叠加多个卷积核在计算上也非常高效。少量的额外计算与显著的表达能力提升使得动态卷积非常适合轻量级的神经网络。
对注意力取值进行限制会简化注意力模型的学习,同时也会缩小多个卷积的叠加核的取值空间。论文将注意力取值限制在0到1之间,同时所有注意力的和为1。如下图所示,假如使用3个卷积核,注意力在0到1之间把叠加核限制在两个三棱锥中,注意力和为1把叠加核进一步限制在以这三个卷积核为顶点的三角形中。对于这两个限制,论文选用了softmax来实现。
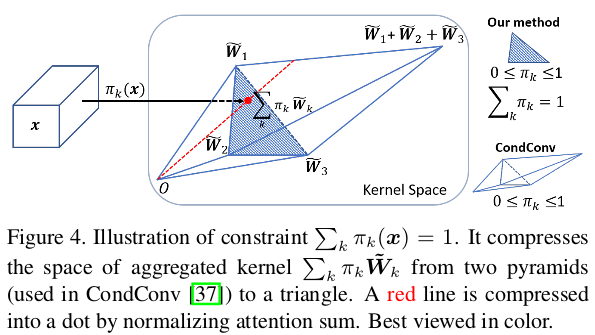
另外,限制注意力取值接近均匀分布有利于多个卷积核在训练初期同时学习。因为softmax会输出更稀疏的注意力,所以论文采用了温度退火(temperature annealing)来提升模型的准确率(接近均匀分布的注意力可以通过使用较大的temperature来实现)。
Dynamic ReLU
通常ReLU和它的一些改进版(Leaky ReLU、PReLU)激活函数的参数都是固定的,所以论文提出了动态ReLU。它可以根据输入特征来调整ReLU的参数。
原版的ReLU为\(y = \max \lbrace x,0\rbrace\),对于输入向量\(x\)的\(c\)维特征,激活值计算为\(y_c = \max \lbrace x_c, 0\rbrace\)。ReLU可统一表示为分段线性函数\(y_c = \max\limits_k \lbrace a^k_cx_c+b^k_c\rbrace\)。基于前面的式子,可以将DY-ReLU定义为多个(\(K\)个)线性函数的最大值。即对所有的输入\(x=\lbrace x_c\rbrace\)自适应\(a^k_c\)、\(b^k_c\)有:
\[ \begin{aligned} y_c &= f_{\theta(x)}(x_c) \\ &= \max\limits_{1\le k\le K}\{a^k_c(x)x_c+b^k_c(x)\} \end{aligned} \]
参数\((a^k_c,b^k_c)\)为超函数\(\theta(x)\)的输出:
\[ \theta(x) = [a^1_1,\dots,a^1_C,\dots,a^K_1,\dots,a^K_C,b^1_1,\dots,b^1_C,\dots,b^K_1\dots,b^K_C]^T \]
其中\(C\)为通道数,激活参数\((a^k_c, b^k_c)\)不仅与\(x_c\)相关,也与\(x_{j\ne c}\)相关,即还与其它通道的输入有关。
论文采用类似于SE模块的轻量级网络进行超函数的实现。对于大小为\(C\times H\times W\)的输入\(x\),首先用全局平均池化来压缩空间信息,之后通过两个全连接层(中间包含ReLU),最后接一个归一化层,归一化层使用\(2\sigma(x)-1\)将结果约束在-1到1之间(\(\sigma\)为Sigmoid函数)。最后一共输出\(2KC\)个元素,分别对应于\(a_{1:C}^{1:K}\)和\(b_{1:C}^{1:K}\)的残差,即\(\Delta a_{1:C}^{1:K}\)和\(\Delta b_{1:C}^{1:K}\)。最终输出为初始值和残差的和:
\[ \begin{aligned} a^k_c(x) &= \alpha^k+\lambda_a\Delta a^k_c(x) \\ b^k_c(x) &= \beta^k+\lambda_b\Delta b^k_c(x) \end{aligned} \]
其中\(\alpha^k\)、\(\beta^k\)为\(a^k_c\)、\(b^k_c\)的初始值。\(\lambda_a\)、\(\lambda_b\)是用于控制残差大小的标量。\(\alpha^k\)、\(\beta^k\)、\(\lambda_a\)、\(\lambda_b\)为超参数且与通道无关,默认情况下,\(\lambda_a=1.0\)、\(\lambda_b=0.5\),故默认情况下的超参数为\(\alpha^{1:K}\)、\(\beta^{1:K}\)。
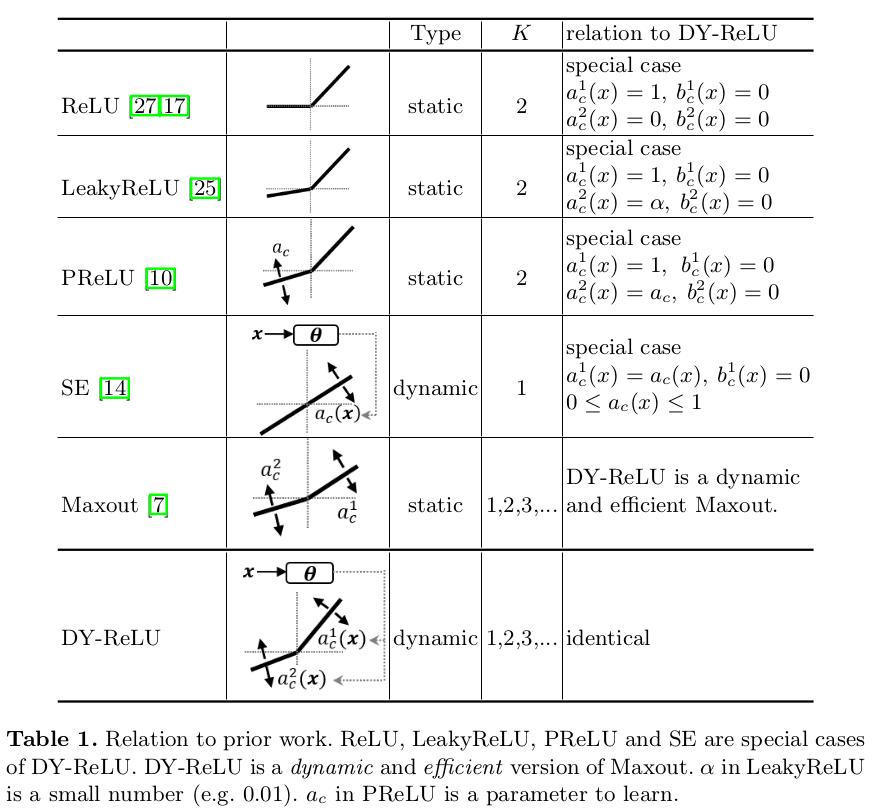
论文还给出了DY-ReLU的三种实现,大致如下:

DY-ReLU-A
空间位置和通道均共享(spatial and channel-shared)。最终输出大小为\(2K\),计算较简单,表达能力也较弱。
DY-ReLU-B
空间位置共享而通道不共享(spatial-shared and channel-wise)。最终输出大小为\(2KC\),即每个通道\(2K\)个。
DY-ReLU-C
空间位置和通道均不共享(spatial and channel-wise)。每个通道的每个元素都有一个独立的激活函数,最终输出的参数为\(2KHWC\),直接使用全连接层会带来大量的额外计算。论文对此进行了改进,如上图所示,将空间位置解藕到另一个注意力分支,最后将通道参数\(a_{1:C}^{1:K}\)、\(b_{1:C}^{1:K}\)乘以空间位置注意力\(\pi_{1:HW}\)。空间位置注意力的计算简单地使用\(1\times 1\)卷积和归一化方法,归一化使用了带约束的softmax函数:
\[ \pi_{h,w} = \min \{\frac{\gamma\exp (z_{h,w}/\tau)}{\sum_{h,w}\exp (z_{h,w}/\tau)}, 1\} \]
其中\(\gamma\)是一个标量,用于扩大softmax的值,以防止梯度消失,论文设置为\(\frac{HW}{3}\)。\(z_{h,w}\)为\(1\times 1\)卷积的输出。\(\tau\)是temperature,一个大的temperature(如\(\tau\) = 10)可用于防止训练早期空间位置注意力过于稀疏。