PointNet、PointNet++和Frustum PointNet。常用的3D点云目标检测。
PointNet
PointNet将深度学习直接应用于点云数据。点云数据是欧式空间下的点的一个子集,有无序性、点与点的空间关系以及不变性这三个性质。
- 无序性。点云数据是一个集合,对数据顺序并不敏感,这要求模型对数据的不同排列保持不变性。有几种思路。首先是将点云按某种规则进行排序,但对于高维空间,很难找到一个稳定的排序规则。另外一种将其作为一种序列使用RNN进行训练,这种方式很难处理好长度极大(成千上万)的输入元素(如点云)。最后作者利用对称函数去聚集每个点的信息:\(f(\lbrace x_1,x_2,\cdots,x_n\rbrace)\approx g(h(x_1),h(h(x_2),\cdots,h(x_n))\),其中等式左侧为目标,右侧为设计的对称函数。由上式可看出对于点云中的各个点,使用\(h\)分别处理,再进入对称函数\(g\)函数处理。论文中作者选用的是\(h\)为MLP,\(g\)就是max pooling。
- 点与点之间的空间关系。一个物体通常由特定空间的点云组成,点与点之间是存在空间关系的,PointNet采用将全局特征与局部特征串联来利用空间关系。
- 不变性。点云数据所代表的目标对一些空间变换(刚性变换)应该具有不变性。PointNet在点云提取特征之前,对点云数据进行对齐来保证不变性。对齐操作是通过训练一个小型网络(T-Net)来得到转换矩阵,并和输入的点云数据相乘来实现的。这部分的操作可以看为是对空间点进行调整,直观上理解是旋转出一个有利于分类或分割的角度(刚性变换),在具体实现时还加入相关损失函数来使转换矩阵接近正交化,以减少点云信息损失。(正则化:\(L_{reg}=\lVert I-AA^T\rVert_F^2\),即L2损失)
PointNet的大致结构如下:
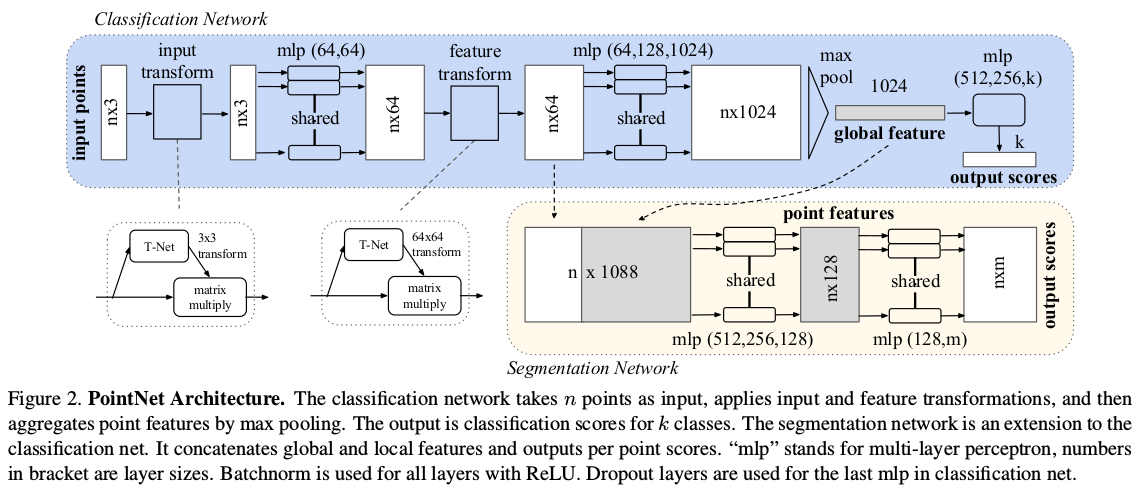
图中包含了分类和分割两部分,其中分割结合了全局池化特征和第二次对齐后的点云特征。源码中分类部分的代码使用了T-Net,分割部分可以不使用,对结果没有太大提升,主要是因为PointNet结构本身不能学习到点与点之间的局部关系,即使添加了T-Net也一样。
PointNet++
PointNet++针对PointNet的一些问题进行了改进。
首先介绍一下基础网络层
- 采样层。通常原始的点云数据数量巨大,对每个点提取局部特征会导致巨大的计算量,为此PoinNet++先对点云进行了采样。使用的采样方法为最远点采样(FPS,Farthest Point Sampling),相对于随机采样,这种采样方式能够更好地覆盖整个采样空间。
- 组合层。为了获取点的局部特征,我们需要获得点的局部范围。在图片中,像素点的局部定义为在其周围一定曼哈顿距离下的像素点。对于点云数据,点的局部定义为在其周围给定半径划出的球形空间中的点。组合层即是找出采样后点云中每个点构成的局部所包含的点,以便进行后续的特征提取。
- 特征提取层。这里借用了PointNet来对各个局部点云提取特征。
以上各层即可构成PointNet++的基础模块。这些基础模块类似于CNN,将多个这样的模块级联起来即可得到PointNet++,可以提取出点云数据的浅层特征到深层特征。针对PointNet的改进点如下:
- PointNet仅仅是对每个点进行特征表达,对局部结构信息的提取能力较差。所以PointNet++使用了sampling层和grouping层来整合局部领域。
- PointNet的global feature直接由max pooling获得,这对于分类和分割任务都会造成较大的信息损失。为此PointNet++通过多个set abstraction(如下图)逐级降采样,获得不同规模不同层次的local-global feature。
- 对于分割任务,PointNet直接将global feature和local feature进行拼接,这样生成的辨别特征较弱,而PointNet++设计了一个encoder-decoder结构来进行分类和分割任务,对于分割部分,先降采样再上采样,并使用skip connection将对应层的local-global feature拼接。
最后模型大致结构如下:
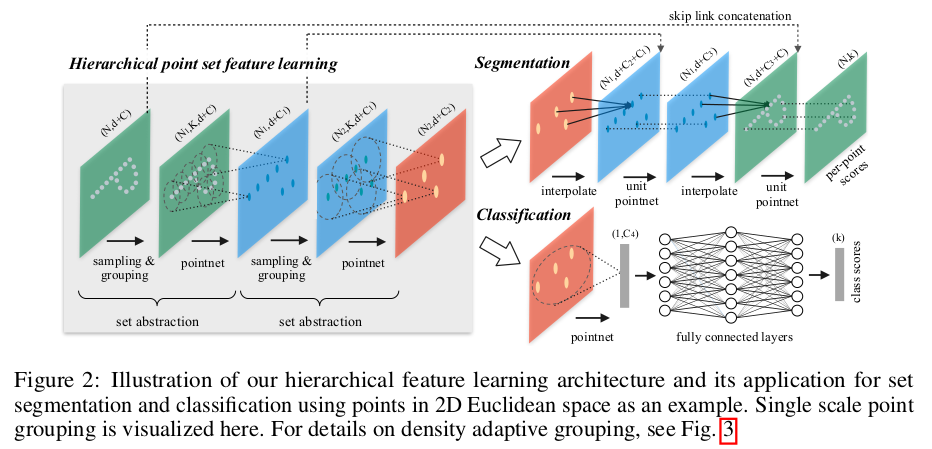
由于点云在空间中的分布是不规则且不均匀的,PointNet++虽然可以学习点云的局部特征,但点云的在各个局部的分布不均匀可能会导致模型不能很好地提取特征。为此,作者采取了两种方法:
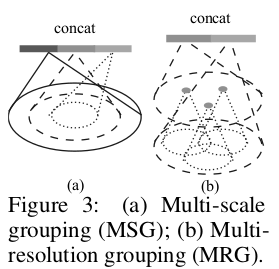
- 多尺度组合(Multi-Scale Grouping,MSG)。即提取不同尺度的局部特征并将它们串联拼接在一起。这种操作方式会增加许多计算量。如下图a所示
- 多分辨率组合(Multi-Resolution Grouping,MRG)。该方法对每个局部提取到的特征都由两个向量串联表示,如下图b所示。第一部分由其前一层提取到的特征再次通过特征提取层得到,第二部分则通过直接对这个局部对应的原始点云数据中的所有点进行特征提取得到。
FPS算法原理:
- 输入点云有\(N\)个点,随机选择一个点\(P_0\)作为起始点,得到采样集\(S=\lbrace P_0\rbrace\);
- 计算所有点到\(P_0\)的距离,构成\(N\)维数组\(L\),从中选择距离最大的点作为采样点\(P_1\),并添加至采样集\(S=\lbrace P_0,P_1\rbrace\);
- 计算所有点到\(P_1\)的距离,对于每个点\(N_i\),若其距离\(P_1\)的距离小于\(L[i]\),则更新距离数组\(L[i]=d(N_i,P_1)\),即数组\(L\)存放的是每个点到采样集\(S\)的最近距离;
- 从\(L\)中选取最大值对应的点加入采样集中\(S=\lbrace P_0,P_1,P_2\rbrace\);
- 重复2-4步,直至采样集长度达到\(n\),即采样了\(n\)个目标点
这里涉及到初始点的选取和距离度量方式的问题,一般如下:
- 初始点选择:
- 随机选择一点,这样每次结果都不同
- 选择距离点云重心距离最远的点,这样每次结果都相同且初始点一般位于局部极值点,有一定的刻画能力
- 距离度量方式:
- 欧式距离,主要针对点云,在3D立体空间均匀采样
- 测地距离,即两顶点沿网格表面最短路径的距离,主要针对三角网格,在三角网格面上进行均匀采样
最后说一下分割任务的decoder。经过前面encoder的处理,我们得到的是少量点的特征表达,为了对点云进行分割,PointNet++使用了一种反向插值来上采样。具体如下:
假设interpolate之前的点云为\(P_1\),维度为\(N_1\times C\);之后的点云为\(P_2\),维度为\(N_2\times C_2\),其中\(N_2\gt N_1\)(因为该操作为上采样)。依据下式进行上采样计算:
\[ \begin{aligned} & f^{(j)}(x)=\frac{\sum_{i=1}^kw_i(x)f_i^{(j)}}{\sum_{i=1}^kw_i(x)} \\ where\qquad &w_i(x)=\frac{1}{d(x,x_i)^p}, \ j=1,2,\cdots,C \end{aligned} \]
即对于\(P_2\)中的每个点\(x\),找到在采样前点云空间\(P_1\)中与其距离最短的\(k\)个点\(x_1,x_2,\cdots,x_k\),对这\(k\)个点的特征进行加权求和即可得\(x\)的特征,其中这个权重是与距离成反相关的,即越远离相应的贡献度越低。这里的距离度量函数为\(d\)。论文中选取的参数为\(p=2\),\(k=3\)。
而以上的操作得到的只是global级别的特征,为了得到准确的分割结构,我们还需要local级别的特征,所以PointNet++还加入了skip connection。操作较简单,即将encoder对应层的点云特征拿过来与当前层进行拼接,之后再经过unit pointnet(一系列mlp)进行整合。具体可参考上面PointNet++网络结构图。
Frustum PointNet
将RGB图像信息与点云信息结合进行检测。主要流程是先通过目标检测模型得到2D图像上的目标框,将目标框映射到3D点云中,得到frustnum proposal,再使用基于点云的模型对frustum proposal区域进行实例分割和3D边界框回归。大致结构如下:
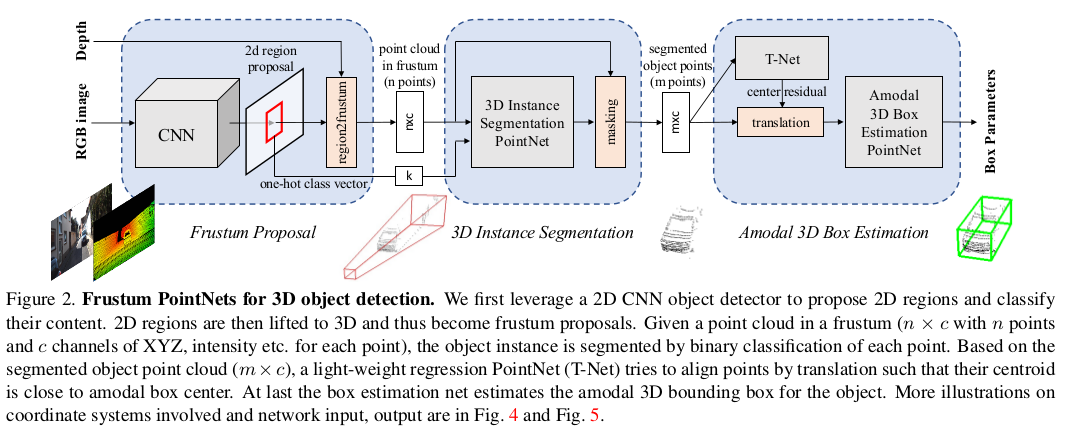
图中第一部分就是2D目标检测网络,得到目标框及其类别,然后将目标框映射为3D的frustum proposal。第二部分是实例分割部分,将上一部分得到的frustum proposal中的点采样到\(N\)个,对应维度为\(N\times C\),与之前得到的类别one-hot向量一起作为实例分割网络的输入,输出一个掩码。最后一部分,将被上一步掩码过滤过的\(M\)个点作为输入,先由T-Net进行校正对齐,然后通过另一个网络回归预测出3D边界框。
在将2D检测框映射到3D点云生成frustum proposal时,由于每个frustum proposal的朝向都不一样,因此论文里将其旋转到与相机正交的方向,增加了后续算法的旋转不变性。如下a到b所示。

仅使用frustum proposal时,得到的点云包含有大量的背景点。所以第二部分的实例分割将前景从背景中分离出来,对于分割出来的前景点还要将其中心化来引入平移不变性,如上图c所示。
实例分割部分虽然得到了目标的中心点,但由于其前景点云可能没能全部包含目标,所以还需要对中心点进行修正。最后一部分使用了T-Net来学习目标中心点的残差。最后Box Estimation Net输出最终3D边界框的各种参数,输出的维度为\(3+4\times NS+2\times NH\),其中3代表对于中心点的残差回归(XYZ),是接在T-Net回归之后的,\(NS\)代表不同size的anchor个数,每个anchor有四个维度,分别是该anchor的置信度以及长宽高的残差回归,\(NH\)代表不同朝向的anchor,每个anchor有两个参数,分别是置信度和朝向角\(\theta\)。
2D检测网络之后模型各部分的详细结构大致如下:(包含有两个版本,分别对应于使用PointNet和PointNet++来提取点云特征)
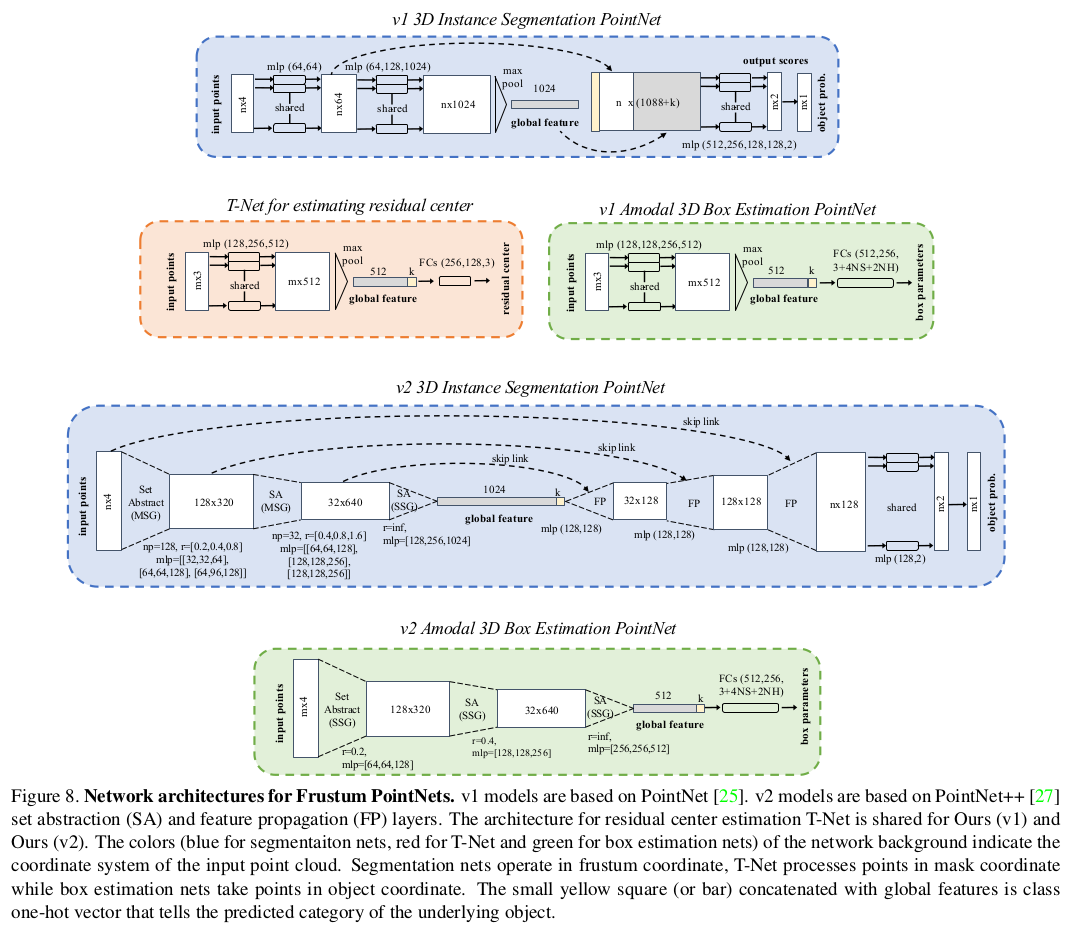
实际中3D边界框的尺寸和角度共同决定了边界框的信息,所以论文还提出了边界框的corner loss:
\[ L_{corner} = \sum_{i=1}^{NS}\sum_{j=1}^{NH}\delta_{ij}min\{\sum_{k=1}^8\vert\vert P_k^{ij}-P_k^\ast\vert\vert, \sum_{i=1}^8\vert\vert P_k^{ij}-P_k^{\ast\ast}\vert\vert\} \]
在\(NS\times NH\)个anchor中,只有正确的size和head朝向的那个边界框才会计算损失(其余情况下\(\delta=0\))。对于第\(i\)个size的第\(j\)个朝向的box的第\(k\)个角\(P_k^{ij}\),会移动到ground truth box的中心,与每个对应的角算L1 Loss。考虑到翻转180度的问题,这里会算与180度旋转之后的角\(P^{\ast\ast}\)的损失,并取最小值。总体损失如下:
\[ L_{multi−task} =L_{seg} + \lambda(L_{c1−reg} + L_{c2−reg} + L_{h−cls} + L_{h−reg} + L_{s−cls} + L_{s−reg} + \gamma L_{corner}) \]
致谢
PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation
PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space