点云有着分布上稀疏、结构上不规则、几何上无序的特性,所以直接在点云上使用卷积操作可能会导致生成的特征极度地偏离它原本的表达。
VoxelNet
该模型是对点云进行体素化,然后利用3D卷积来获取特征。具体是:
- 将点云空间均分为大小为\(v_D\)、\(v_H\)、\(v_W\)的体素网格,并且同一网格内随机保留最多\(T\)个点(多的剔除,少的不管)。
- 对体素单元使用VFE层(voxel feature encoding layer)来提取体素特征并合并为一个4D的张量。
- 在上面得到的张量上使用3D卷积进一步提取特征,之后用RPN结构来获得结果
如下图:
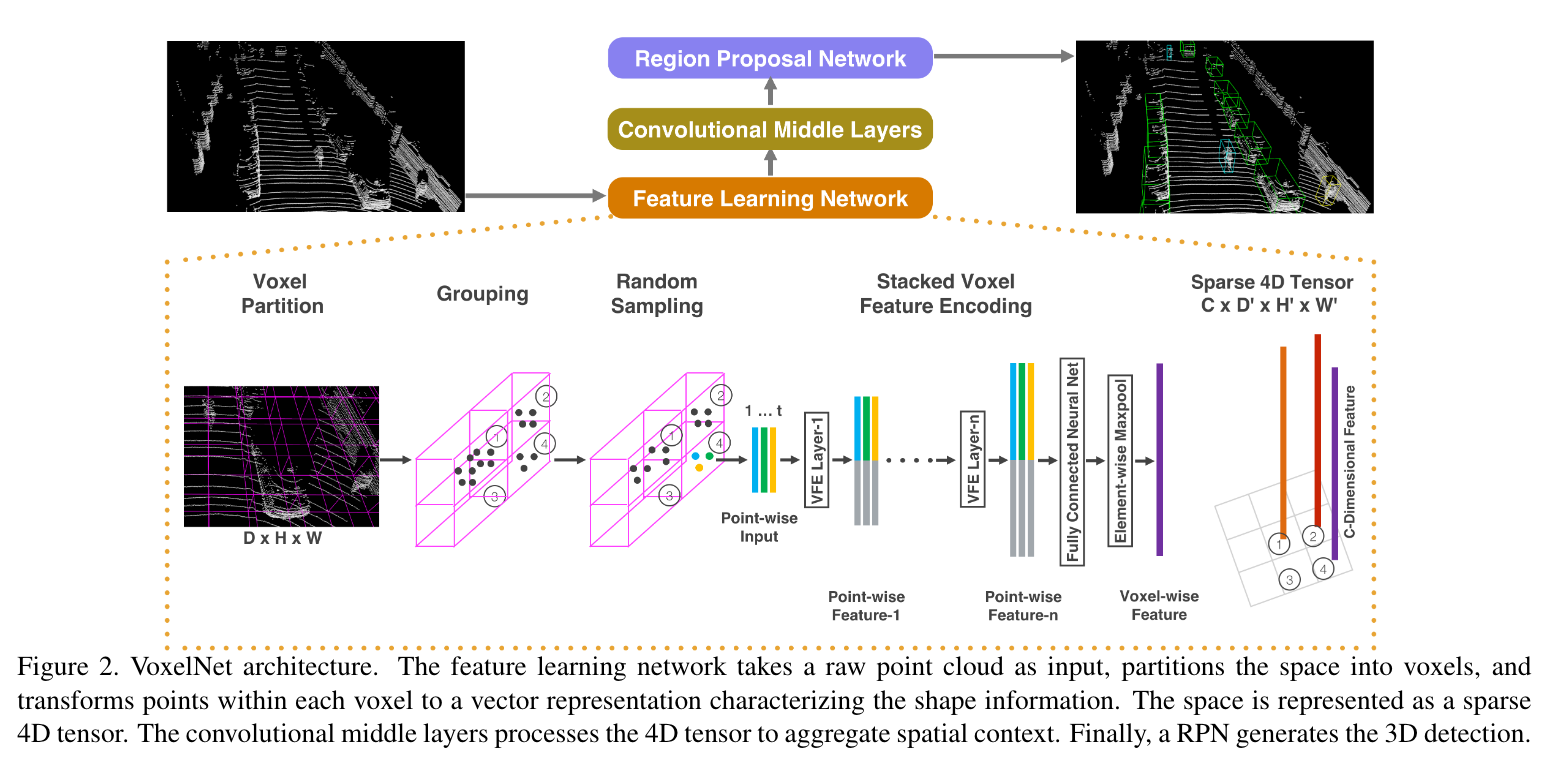
VFE
VFE是VoxelNet里的最重要的一个结构。针对单一层的VFE,主要有下面几步操作:
- 计算体素内所有点的坐标均值并计算它们到均值的偏差即可得到点的输入特征,合并在一起作为VFE的输入特征\(\mathbf{V}_{in} = \{\hat{\mathbf{p}}_i = [x_i, y_i, z_i, r_i, x_i-v_x, y_i-v_y, z_i-v_z]^T \in \mathbb{R}^7\}_{i=1\dots t}\)
- 将每个\(\hat{\mathbf{p}}_i\)经过一个由全连接层、BN层和ReLU层组成的FCN结构获得点的特征\(f_i \in \mathbb{R}^m\)
- 对\(V_{in}\)中的所有点的特征使用逐元素MaxPooling获得一个聚合特征\(f \in \mathbb{R}^m\)。这里的element-wise
maxpooling可以理解为
np.max(f, axis=0),这样一个输入大小为(n_point_in_voxel, m)的特征,经过element-wise maxpooling后得到的特征大小为(1, m) - 将\(f\)和\(f_i\)进行拼接即可得到每个点的最后特征\(f^{out}_i = [f^T_i, f^T]^T \in \mathbb{R}^{2m}\)。将体素内的每个点的\(f^{out}_i\)合并在一起就是VFE的最终输出特征\(V_{out}=\{f^{out}_i\}_{i=1\dots t}\)
具体的结构图如下:
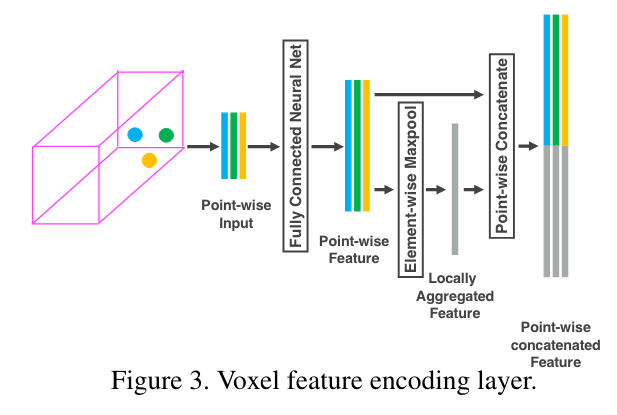
这种逐点的操作可能没能发挥出计算设备的全部性能,所以论文后面也提及到了有关VFE的高效实现方式,具体可以参考原论文。
RPN
经过VFE得到的特征后会使用多个由3D卷积、BN层、ReLU层组成的结构进一步提取特征。最后通过如下的RPN结构来获得最终输出:

SECOND
VoxelNet中使用了3D卷积层,这个卷积层计算量大导致模型整体的推理速度较慢。该论文提出了一个稀疏3D卷积操作方法,同时针对VoxelNet对于目标的方向不敏感问题提出了angle loss regression。
关于稀疏3D卷积方法或者SECOND,网上的文章有了很详细的说明,重点在于建立起输入输出的元素索引表。这里我推荐两篇:
Data Augmentation
SECOND中特意花了大概半页的篇幅来说明了他们使用的一些数据增强方法。
Sample Ground Truths from the Database
由于点云ground truth的数据比较稀缺,所以模型训练的收敛速度以及最终性能都收到了很大的限制。作者通过了类似小目标粘贴的数据增强方法来增强点云数据。
- 利用现有数据生成一个带有点云和相应ground truth的database
- 通过拼接将database中的目标引入到当前点云数据中
- 在移除和拼接目标时使用碰撞检测来校验当前操作是否符合物理规则
这种方法可以有效地增加点云中ground truths的目标数量,同时也可以提升数据的多样性。
Object Noise
与VoxelNet中的类似,即独立、随机地去给点云中的目标添加噪声。但VoxelNet是对所有点都用相同的参数,而作者会在\(\Delta\theta \in [-\pi/2, \pi/2]\)中随机选取一个值用于随机旋转操作,在均值为0,标准差为1的高斯分布上随机选取一个值用于随机线性变换。
Global Rotation and Scaling
对整个点云数据和相应的标注框进行缩放和旋转,缩放的尺度范围为\([0.95, 1.05]\),旋转的范围为\([-\pi/4, \pi/4]\)。
参考
VoxelNet: End-to-End Learning for Point Cloud Based 3D Object Detection