单目3D检测在自动驾驶领域是一个重要且充满挑战的任务,目前的难点是如何准确对目标深度进行预测。MonoRCNN利用几何关系将深度估计问题解耦为目标实际高度和在图像上的投影高度问题。
作者给这个模型的使用限定了两个条件:
- 模型只预测目标的航向角,即yaw角
- 在训练和推理阶段,相机内参已知
Architecture
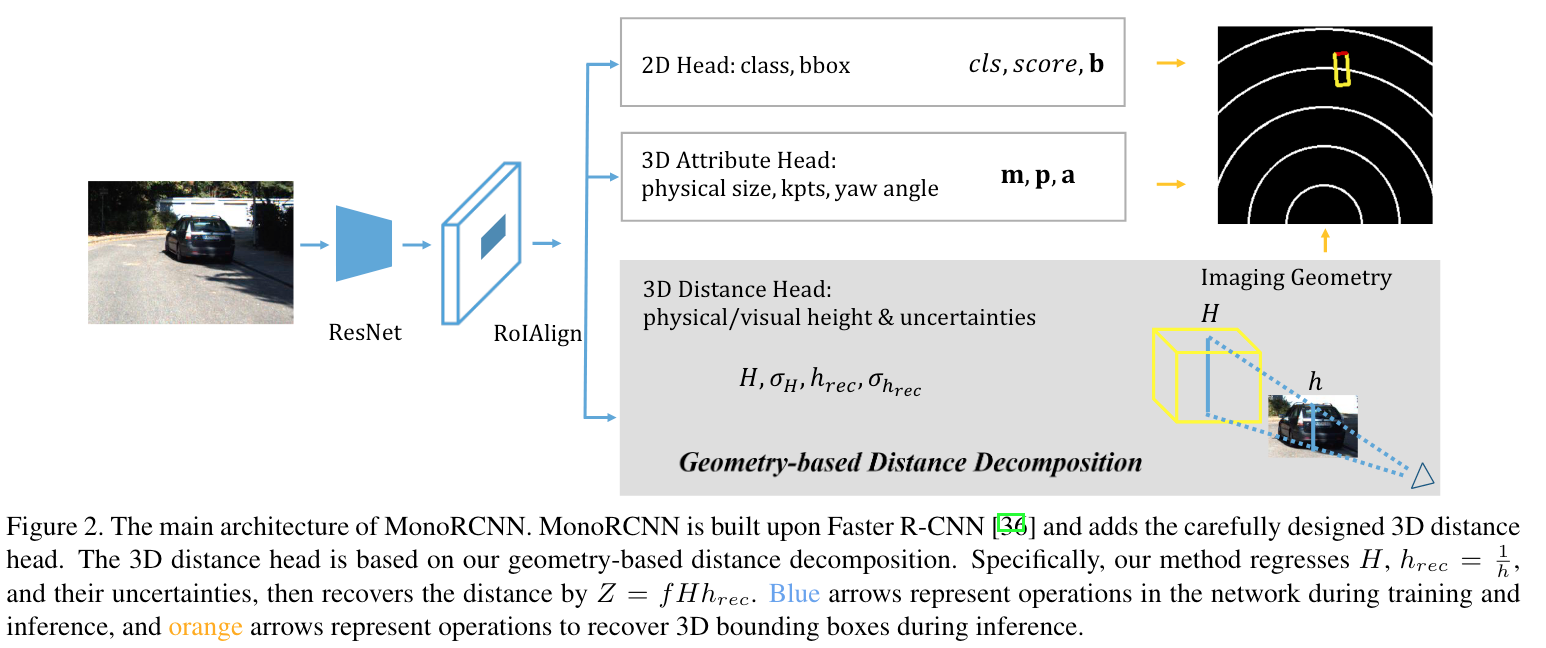
模型类似于Faster R-CNN,backbone采用ResNet-50和FPN结合的形式,之后使用RoIAlign来截取目标特征,然后就接了三个分支:2D head、3D attribute head、3D distance head。最终预测得到以下参数:
- class label \(cls\)和confidence \(score\)
- 2D bounding box \(\mathbf{b} = (x_1, y_1, x_2, y_2)\),使用左上角和右下角坐标表示
- 3D bounding box的中心点在图像上的投影坐标 \(\mathbf{p} = (p_1, p_2)\)
- 3D bounding box的物理尺寸 \(\mathbf{m} = (W, H, L)\),分别表示目标真实的宽、高和长
- 3D bounding box的yaw角 \(\mathbf{a} = (sin\theta, cos\theta)\)
- 3D bounding box中心点的深度\(Z\)
MonoRCNN预测出在图像坐标系下的3D bounding box中心坐标\((p_1, p_2, Z)\),之后借助相机内参矩阵\(\mathbf{P}\)转为相机坐标下的点:
\[ \begin{bmatrix} p_1 \cdot Z \\ p_2 \cdot Z \\ Z \end{bmatrix}_P = \mathbf{P} \cdot \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}_C \]
3D Distance Head
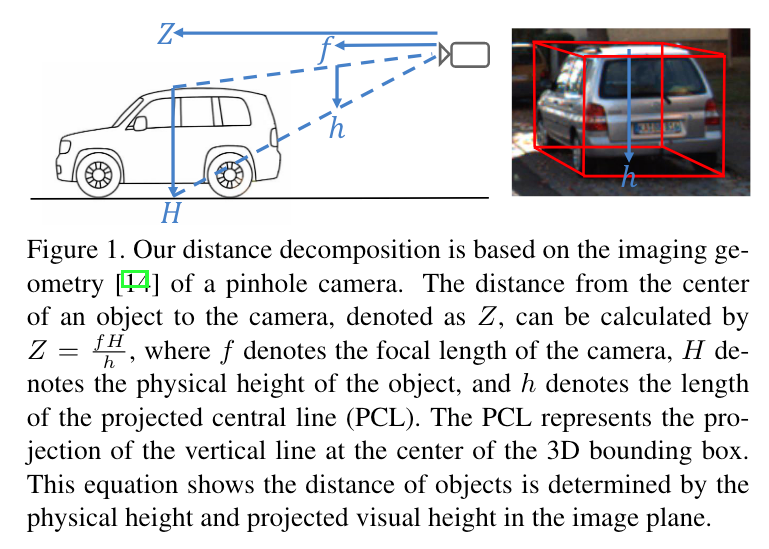
如上图,由简单的几何关系可以得到:
\[ Z = \frac{fH}{h} = fHh_{rec} \]
其中\(h_{rec} = \frac{1}{h}\)。作者通过回归预测\(H\)和\(h_{rec}\)来间接得到\(Z\)。由于只需要获取图像上的目标高度,所以该方法可以有效地应对遮挡、反光、目标被截断等复杂场景。同时,这种解耦方式还保持了自洽性(self-consistency),从而在两个预测高度都不准确的情况下仍能准确地预测出深度,例如预测出的\(H\)较大时,模型会自适应地减小\(h_{rec}\)。这部分具体的内容建议参考原论文。
这个分支的损失函数采用的是uncertainty-aware regression loss:
\[ \begin{aligned} L_H &= \frac{L_1(\hat{H}, H)}{\sigma_H} + \lambda_Hlog(\sigma_H) \\ L_{h_{rec}} &= \frac{L_1(\hat{h}_{rec}, h_{rec})}{\sigma_{h_{rec}}} + \lambda_{h_{rec}}log(\sigma_{h_{rec}}) \end{aligned} \]
其中\(\hat{H}\)和\(\hat{h}_{rec}\)是ground truths,\(H\)和\(h_{rec}\)是预测值,\(\lambda_H\)和\(\lambda_{h_{rec}}\)为正的系数用于平衡不确定项,\(\sigma_H\)和\(\sigma_{h_{rec}}\)是不确定性的可学习变量。
作者实验证明\(\sigma_{h_{rec}}\)相比\(\sigma_H\)对不同距离的目标更具有判别性,且\(fH\sigma_{h_{rec}}\)可以表示距离的不确定性。所以作者使用\(\frac{score}{fH\sigma_{h_{rec}}}\)来代替\(score\)对预测结果进行排序以提升模型准确率。
3D Attribute Head
这个分支主要预测目标的物理尺寸,yaw角以及2D关键点。对于物理尺寸和yaw角,直接使用L1损失进行回归:
\[ \begin{aligned} L_{size} &= L_1(\hat{\mathbf{m}}, \mathbf{m}) \\ L_{yaw} &= L_1(\hat{\mathbf{a}}, \mathbf{a}) \end{aligned} \]
对于2D关键点,定义:\(\hat{\mathbf{t}} = \left ( \frac{\hat{p}_1 - x_1}{x_2 - x_1}, \frac{\hat{p}_2 - y_1}{y_2 - y_1} \right )\),有:
\[ L_{kpt} = L_1(\hat{\mathbf{t}}, \mathbf{t}) \]
最后,模型的整体损失如下:
\[ \begin{aligned} L =& \lambda_{cls}L_{cls} + \lambda_{bbox}L_{bbox} + \lambda_{size}L_{size} \\ &+ \lambda_{yaw}L_{yaw} + \lambda_{kpt}L_{kpt} + \lambda_HL_H + \lambda_{h_{rec}}L_{h_{rec}} \end{aligned} \]
其中\(\lambda_{cls}=1\)、\(\lambda_{bbox}=1\)、\(\lambda_{size}=3\)、\(\lambda_{yaw}=5\)、\(\lambda_{kpt}=5\)、\(\lambda_{H}=0.25\)、\(\lambda_{h_{rec}}=1\)
参考
Geometry-based Distance Decomposition for Monocular 3D Object Detection