Note: VAE并不是一个只关注重建的模型,它更重要的能力是图像生成,所以VAE并不是一个AE模型,它具备生成能力。
与常见的Autoencoder不同,变分自编码器并不是将输入映射为一个固定的向量,而是映射为一个分布\(p_\theta\)(参数为\(\theta\))。输入数据\(\mathbf{x}\)与隐变量\(\mathbf{z}\)的关系如下:
- \(p_\theta(\mathbf{z})\):先验概率
- \(p_\theta(\mathbf{x}\vert\mathbf{z})\):似然概率
- \(p_\theta(\mathbf{z}\vert\mathbf{x})\):后验概率
假设在获得模型最佳参数\(\theta^{\star}\)后,我们可以通过以下步骤生成符合真实数据分布的样本:
- 从先验概率\(p_{\theta^\star}(\mathbf{z})\)中采样一个\(\mathbf{z}^{(i)}\)
- 依据条件概率\(p_{\theta^\star}(\mathbf{x}\vert\mathbf{z}=\mathbf{z}^{(i)})\)生成\(\mathbf{x}^{(i)}\)
最优参数\(\theta^\star\)可以通过最大化恢复真实数据分布的概率得到:
\[ \theta^\star = argmax_\theta\prod_{i=1}^np_\theta(\mathbf{x}^{(i)}) \]
转为对数空间可得:
\[ \theta^\star = argmax_\theta\sum\log p_\theta(\mathbf{x}^{(i)}) \]
为了引入encoding vector有:
\[ p_\theta(\mathbf{x}^{(i)}) = \int p_\theta(\mathbf{x^{(i)}}\vert\mathbf{z})p_\theta(\mathbf{z})d\mathbf{z} \]
依据上式,我们需要遍历所有\(\mathbf{z}\)来计算,所以实际上\(p_\theta(\mathbf{x}^{(i)})\)很难得到。作者采用了近似分布的方式来解决这个问题,即对于每个输入样本\(\mathbf{x}\),引入了一个由参数\(\phi\)表达的分布\(q_\phi(\mathbf{z}\vert\mathbf{x})\)来直接去近似后验概率分布\(p_\theta(\mathbf{z}\vert\mathbf{x})\)。这样可以保证输入样本、隐变量和重构样本是一一对应的。所以最终VAE的结构与Autoencoder就比较类似了:
- 由近似后验概率\(q_\phi(\mathbf{z}\vert\mathbf{x})\)来得到隐变量,即encoder部分。\(q_\phi(\mathbf{z}\vert\mathbf{x})\)也称为probabilistic encoder。
- 由似然概率\(p_\theta(\mathbf{x}\vert\mathbf{z})\)来生成结果,即相当于decoder部分。\(p_\theta(\mathbf{x}\vert\mathbf{z})\)也称为probabilistic decoder。
我们期望近似分布\(q_\phi(\mathbf{z}\vert\mathbf{x})\)与\(p_\theta(\mathbf{z}\vert\mathbf{x})\)能够尽可能相似。一个自然的想法是最小化它们之间的KL散度\(D_{KL}(q_\phi(\mathbf{z}\vert\mathbf{x})\vert\vert p_\theta(\mathbf{z}\vert\mathbf{x}))\)。将\(D_{KL}\)展开化简可得:
\[ \begin{aligned} & D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \vert\vert p_\theta(\mathbf{z}\vert\mathbf{x}) ) \\ =& \log p_\theta(\mathbf{x}) + D_\text{KL}(q_\phi(\mathbf{z}\vert\mathbf{x}) \vert\vert p_\theta(\mathbf{z})) - \mathbb{E}_{\mathbf{z}\sim q_\phi(\mathbf{z}\vert\mathbf{x})}\log p_\theta(\mathbf{x}\vert\mathbf{z}) \end{aligned} \]
即:
\[ \begin{aligned} & \log p_\theta(\mathbf{x}) - D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \vert\vert p_\theta(\mathbf{z}\vert\mathbf{x}) ) \\ =& \mathbb{E}_{\mathbf{z}\sim q_\phi(\mathbf{z}\vert\mathbf{x})}\log p_\theta(\mathbf{x}\vert\mathbf{z}) - D_\text{KL}(q_\phi(\mathbf{z}\vert\mathbf{x}) \vert\vert p_\theta(\mathbf{z})) \end{aligned} \]
最大化上式就是我们的优化目标,即最大化生成真实数据分布的似然概率,同时最小化近似后验分布与真实后验分布的KL散度。取负号可得损失函数:
\[ \begin{aligned} L_\text{VAE}(\theta, \phi) &= -\log p_\theta(\mathbf{x}) + D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \vert\vert p_\theta(\mathbf{z}\vert\mathbf{x}) )\\ &= - \mathbb{E}_{\mathbf{z} \sim q_\phi(\mathbf{z}\vert\mathbf{x})} \log p_\theta(\mathbf{x}\vert\mathbf{z}) + D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \vert\vert p_\theta(\mathbf{z}) ) \\ \theta^{*}, \phi^{*} &= \arg\min_{\theta, \phi} L_\text{VAE} \end{aligned} \tag{1} \]
由于KL散度是非负的,即有:
\[ -L_\text{VAE} = \log p_\theta(\mathbf{x}) - D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}\vert\mathbf{x}) ) \leq \log p_\theta(\mathbf{x}) \]
故通过最小化\(L_\text{VAE}\),我们可以最大化生成真实数据样本概率的下界。\(L_\text{VAE}\)也被称为变分下限(VLB,variational lower bound)或证据下限(ELBO,evidence lower bound)。
从上面(1)式中可以看到计算损失函数时需要对分布\(q_\phi(\mathbf{z}\vert\mathbf{x})\)进行采样,而随机采样过程并不能去计算梯度。VAE论文中采用重参数化技巧(reparameterization trick)将采样过程的随机性转移到其它变量上:
\[ \begin{aligned} \mathbf{z} &\sim q_\phi(\mathbf{z}\vert\mathbf{x}^{(i)}) = \mathcal{N}(\mathbf{z}; \boldsymbol{\mu}^{(i)}, \boldsymbol{\sigma}^{2(i)}\boldsymbol{I}) & \\ \mathbf{z} &= \boldsymbol{\mu} + \boldsymbol{\sigma} \odot \boldsymbol{\epsilon} \text{, where } \boldsymbol{\epsilon} \sim \mathcal{N}(0, \boldsymbol{I}) & \scriptstyle{\text{; Reparameterization trick.}} \end{aligned} \]
即先从标准正态分布随机采样一个样本\(\mathbf{\epsilon}\),然后乘以VAE encoder部分预测的标准差,再加上encoder预测的均值,这样就能计算该损失对VAE encoder网络参数的梯度了。
\(L_\text{VAE}\)也可以看成是重建损失和正则化两项的和,其中第一项\(\mathbb{E}_{\mathbf{z}\sim q_\phi(\mathbf{z}\vert\mathbf{x})}\)对应的是重建损失,而\(D_{KL}\)则相当于是一个KL正则项。依据数据类型的不同,损失中第一项包含的\(p_\theta(\mathbf{x}\vert\mathbf{z})\)分布也是不同的,最终得到的重建损失也是不同的。例如当\(p_\theta(\mathbf{x}\vert\mathbf{z})\)是一个各分量独立的多元高斯分布时,代入相关的表达式得到重建损失就是一个L2损失,而当该分布是一个伯努利分布时,得到的重建损失为交叉熵。
这里有个小注意点。由于KL散度是不对称的,所以为何我们是去最小化\(D_{KL}(q_\phi\vert\vert p_\theta)\)而不是\(D_{KL}(p_\theta\vert\vert q_\phi)\)呢?(具体可以参考这篇文章)
\(D_{KL}(p_\theta\vert\vert q_\phi)\)又被称为Forward KL,而\(D_{KL}(q_\phi\vert\vert p_\theta)\)称为Reversed KL。对Forward KL展开有:
\[ D_{KL}(p_\theta\vert\vert q_\phi) = \sum_z p_\theta(z)\log\frac{p_\theta(z)}{q_\phi(z)} \]
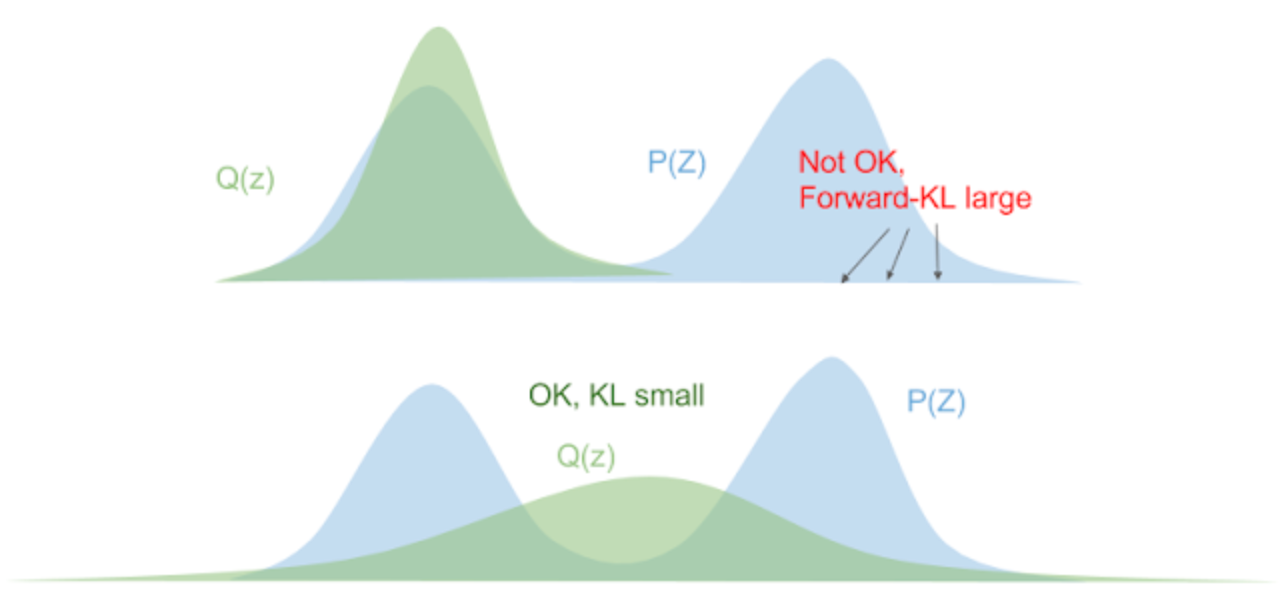
对任意\(p_\theta(z) \gt 0\),有\(\lim_{q_\phi(z) \to 0} \log \frac{p_\theta(z)}{q_\phi(z)} \to \infty\),这意味着当\(q_\phi\)不能覆盖\(p_\theta\)时,Forward KL的值会变得非常大。所以最后得到的\(q_\phi\)会覆盖整个\(q_\theta\),如下图:
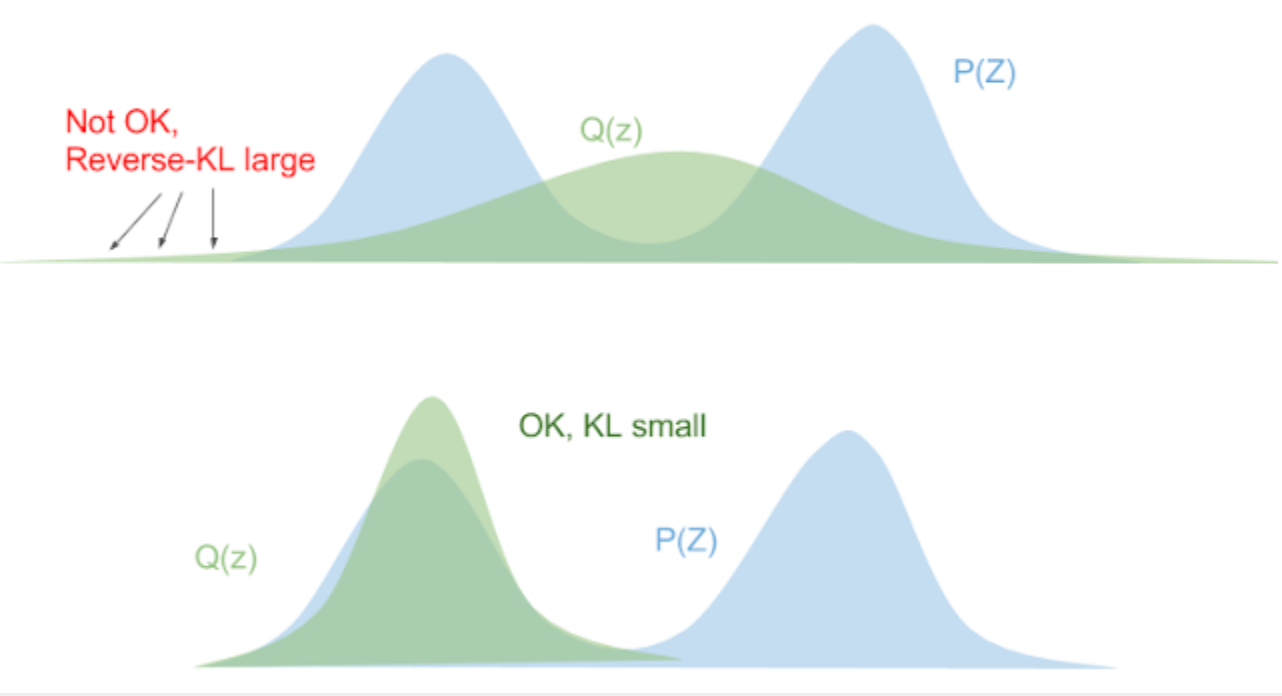
对Reversed KL展开有:
\[ D_{KL}(q_\phi\vert\vert q_\theta) = \sum_z q_\phi(z)\log \frac{q_\phi(z)}{p_\theta(z)} \]
上式当\(p_\theta(z)\)为0时,\(q_\phi(z)\)也必须为0,不然KL散度的值会出现异常。所以最后得到的\(q_\phi\)会被压缩在\(p_\theta\)范围内,如下图: