VQGAN是一个可以在多种图像生成任务上(如无条件图像生成、图像补全、条件引导图像生成等)均有着良好性能的生成模型,其中最大的亮点在于超像素级别的图像生成(百万级像素)。
模型整体流程图如下:
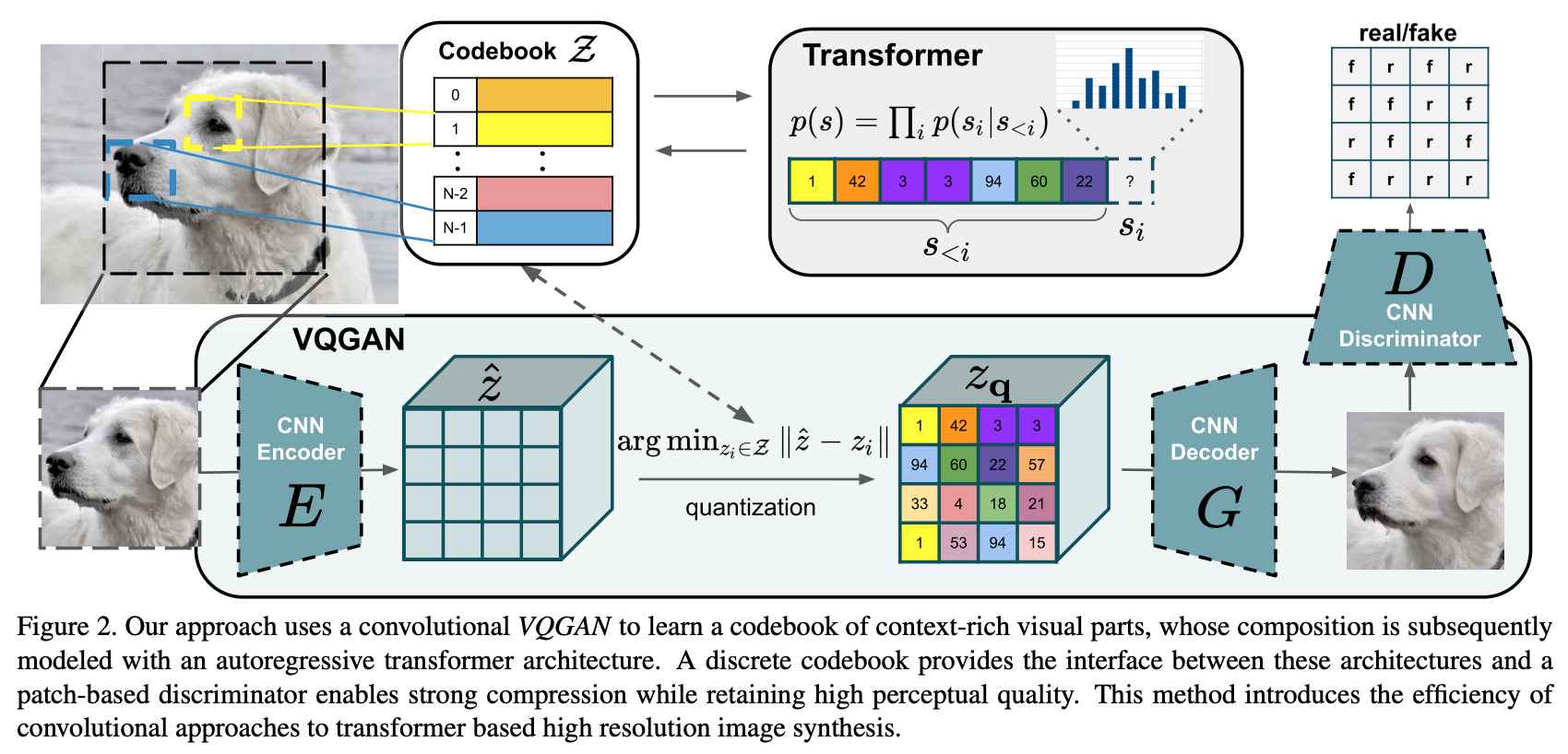
整体上来说与VQVAE相近,但是将VQVAE中的PixelCNN替换为Transformer,同时在训练过程中加入PatchGAN的判别器做对抗损失。
损失函数
在VQVAE中,其损失函数可以表示如下:
\[ \begin{aligned} L_{VQ}(E,G,Z) &= L_{rec} + \vert\vert\text{sg}[E(x)] - z_q\vert\vert_2^2 + \vert\vert\text{sg}[z_q] - E(x)\vert\vert_2^2 \\ &= \vert\vert x - \hat{x}\vert\vert_2^2 + \vert\vert\text{sg}[E(x)] - z_q\vert\vert_2^2 + \vert\vert\text{sg}[z_q] - E(x)\vert\vert_2^2 \end{aligned} \]
其中\(E,G,Z\)分别代表encoder、decoder和codebook。\(\text{sg}\)是stop gradient操作。\(L_{rec}\)是重建损失。
在VQGAN中,作者将\(L_{rec}\)替换为感知损失(perceptual loss),同时还加入了GAN中的对抗loss。在实际应用中,为了在某一任务上实现更好的效果,可能会出现L2损失与感知损失一同使用的情况,甚至是将L2损失替换为L1损失,需要按照具体任务通过实验确定。
Perceptual loss
在一些图像风格迁移、超分辨率等的任务中,传统的损失函数pixel-loss(如L1、L2或cross entropy等)都是追求模型输出与目标在像素级上相等,但像素值上一个很小的偏差,在实际效果上基本没有区别,而pixel-loss的值却会很大。感知损失主要关注图像的风格、颜色以及纹理之类的特征,可以更好地反映模型优化目标。
该损失函数的计算需要借助额外的网络来提取特征,具体计算流程大致如下:
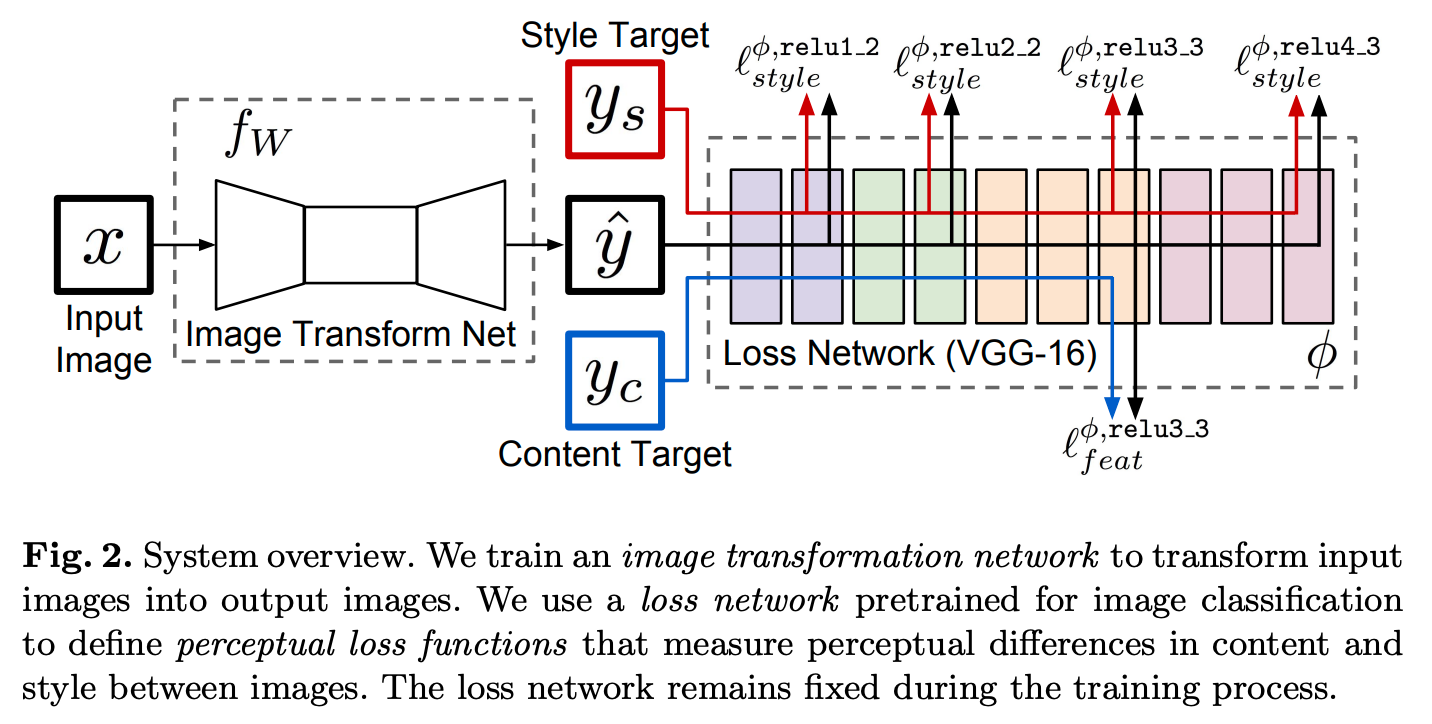
上图中的\(f_W\)对应的是我们需要训练的模型。VGG-16是在Imagenet上预训练好的模型,主要用来提取特征,不参与权重更新。感知损失分为两部分:content loss和style loss。
content loss就是在feature层上的L2损失。选择在feature层上而不是原图上去做是为了避免output与target过分相似,同时还保留有指导output中content更新的能力。数学表达如下:
\[ L^{\phi, j}_{feat}(\hat{y}, y) = \frac{1}{C_jH_jW_j}\vert\vert \phi_j(\hat{y}) - \phi_j(y)\vert\vert_2^2 \]
其中\(\phi_j(\hat{y})\)和\(\phi_j(y)\)分别代表模型输出\(\hat{y}\)和目标\(y\)在VGG-16网络中第\(j\)层的输出特征,且有\(\phi_j(\hat{y}), \phi_j(y)\in\mathbb{R}^{H_j\times W_j\times C_j}\)。由上图可以看出,论文中提取的特征层为relu3_3的输出。
style loss用来计算图像在风格、颜色、纹理等方面的不同。假设\(\phi_j(x)\in\mathbb{R}^{H_j\times W_j\times C_j}\)表示输入\(x\)在模型\(\phi\)中第\(j\)层网络的输出特征。这里先定义一个格拉姆矩阵(Gram matrix)\(G_j^\phi(x)\),大小为\(C_j\times C_j\):
\[ G_j^\phi(x)_{c,c^\prime} = \frac{1}{C_jH_jW_j}\sum^{H_j}_{h=1}\sum^{W_j}_{w=1}\phi_j(x)_{h,w,c}\phi_j(x)_{h,w,c^\prime} \]
实际计算中我们可以将\(\phi_j(x)\)reshape为\(\psi\in\mathbb{R}^{C_j\times H_jW_j}\),则格拉姆矩阵的计算可以简化如下:
\[ G^\phi_j(x) = \frac{\psi\psi^T}{C_jH_jW_j} \]
style loss则是定义在格拉姆矩阵上的Frobenius范数距离:
\[ L_{style}^{\phi,j}(\hat{y},y) = \vert\vert G_j^\phi(\hat{y}) - G_j^\phi(y)\vert\vert_F^2 \]
格拉姆矩阵计算输出的大小只与输入的通道数有关(输出大小为\(C_j\times C_j\)),所以只要保证通道数相同,即使模型输出与目标的尺寸不一致也是可以计算损失的。
在特征提取网络中,不同深度的卷积层提取的特征是不一样的(低层网络会提取一些点线特征,高层网络会提取一些抽象特征),所以为了能综合评估模型的style能力,我们需要提取各个不同的网络层输出来计算style损失。依据上图。作者分别提取了relu1_2、relu2_2、relu3_3和relu4_3这四层的输出特征去计算style损失,最终求和作为style loss的值。
关于Frobenius范数,其计算公式如下(\(A\in\mathbb{R}^{m\times n}\)):
\[ \vert\vert A\vert\vert_F = \sqrt{\sum^m_{i=1}\sum^n_{j=1}\vert a_{ij}\vert^2} = \sqrt{\text{trace}(A^\star A)} = \sqrt{\sum_{i=1}^{\min(m,n)}\sigma_i^2} \]
上面给出了Frobenius范数的三种计算方式。其中\(A^\star\)表示\(A\)的共轭转置矩阵(共轭转置矩阵在将行与列对换后还要将每个元素共轭一下,实数矩阵的共轭转置矩阵就是转置矩阵),\(\sigma_i\)则是\(A\)的奇异值,且使用了迹函数。
Adversarial loss
关于对抗损失部分,作者选用的是适用于GAN的Hinge loss。一般的Hinge loss通常用于最大边际分类器(maximal margin classifer)如支持向量机中,通过尽可能地拉大模型正负样本之间的得分差距来提高模型性能。数学表示如下:
\[ L = \max(0, 1-\hat{y}y) \]
其中\(\hat{y}\)表示模型输出的样本得分,\(y\)表示样本真实标签(1或-1)。
- 当\(\hat{y}\)与\(y\)同号,即模型分类类别与真实类别相同。此时若\(\vert\hat{y}\vert\le 1\),则表示此时的间距还不够大,损失函数不为0,还会继续更新,直到\(\vert\hat{y}\vert\gt 1\)损失函数为0
- 当\(\hat{y}\)与\(y\)异号,即模型分类类别与真实类别不同,损失函数不为0
在Geometric GAN中,引入了Hinge loss且变换为以下形式:
\[ \begin{aligned} L(G,D) &= L(G) + L(D) \\ &= -E(D(G(z))) + E(\max(0, 1-D(x))) + E(\max(0, 1+D(G(z)))) \end{aligned} \]
Hinge loss主要应用在了判别器\(D\)上。只有当\(D(x)\lt 1\)的真实样本和\(D(G(z))\gt -1\)的生成样本会产生损失,即只有一些被不合理划分的样本会有贡献,这样GAN模型的训练会更加稳定。
在VQGAN中,对抗损失笼统地表示如下:
\[ L_{GAN}(\{E,G,Z\}, D) = [\log(D(x)) + \log(1-D(\hat{x}))] \]
我们的目标是求得最优的\(E, G, Z\),最后总结的优化目标如下:
\[ Q^\star = argmin_{E,G,Z}\max_D\mathbb{E}_{x\sim p(x)}[L_{VQ}(E,G,Z) + \lambda L_{GAN}(\{E,G,Z\}, D)] \]
其中\(\lambda\)是自适应权重,表达式如下:
\[ \lambda = \frac{\nabla_{G_L}[L_{rec}]}{\nabla_{G_L}[L_{GAN}]+\delta} \]
\(L_{rec}\)就是感知损失,\(\nabla_{G_L}[\cdot]\)是一个函数,表示该函数的输入相对于模型decoder最后一层\(L\)的梯度,\(\delta=10^{-6}\)是为了防止除0错误。
VQGAN中新加的判别器\(D\)结构是PatchGAN的判别器,它是一个全卷积的模型结构。通常的GAN判别器输出的只是一个值,而PatchGAN判别器输出的是一个\(n\times n\)的矩阵,矩阵中的每个值都代表输入模型在图像中对应的每个小区域(patch)的得分。这种设计可以让模型更关注图像的细节,也不再是用单单一个值来评价图像的真实性。
随机图像生成
上面的优化目标其实已经可以完成模型各个模块的训练了,但在随机图像生成任务中,我们是需要在没有encoder的情况下,采样出\(z_q\)给到decoder的。VQVAE的方法通过PixelCNN来预测\(z_q\)。考虑到Transformer具有长距离注意力,并且这个采样过程也是可以类比文本序列预测问题,所以作者采用了Transformer结构的模型来预测\(z_q\)(具体结构是GPT-2)。
将采样过程视为自回归预测,即让模型去预测分布\(p(s)=\prod_i p(s_i\vert s_{\lt i})\),相应的损失函数是最大化对数似然函数:
\[ L_{Transformer} = \mathbb{E}_{x\sim p(x)}[-\log p(s)] \]
Transformer模块的训练是需要在其它模块训练好后进行的,具体的训练过程如下:
- 输入经过encoder和codebook后得到\(z_q\in \mathbb{R}^{h\times w\times n}\)并展开为二维形式\(z_q^\prime\in \mathbb{R}^{hw\times n}\),即得到\(hw\)个维度为\(n\)的编码。定义此时\(z_q^\prime\)中的编码组合对应到codebook中的索引为unmodified_indices
- 将\(z_q^\prime\)中的部分编码替换为随机生成的编码(维度依然为\(n\)),定义修改后的编码组合对应的索引为modified_indices。替换为随机编码这一步相当于是在特征中添加了噪声,以此来提升Transformer的泛化性
- 将modified_indices输入到Transformer模型中,通过交叉熵损失训练模型,使其重构出unmodified_indices
借助于Transformer,VQGAN实现了超像素级的图像生成任务。
参考
Taming Transformers for High-Resolution Image Synthesis
Perceptual Losses for Real-Time Style Transfer and Super-Resolution
Image-to-Image Translation with Conditional Adversarial Networks