正常来说图像的像素值是离散的(在0到255之间),所以我们其实可以把图像看成是一个长为\(H\times W\times C\)的序列,在预测当前像素值时,把之前的像素值作为已知信息参与到预测中,这样递归地逐像素预测下去,即自回归模型(autoregressive model):
\[ p(x) = p(x_1)p(x_2\vert x_1)\dots p(x_n\vert x_1,x_2,\dots,x_{n-1}) \]
但上面这一过程是逐像素生成的,所以运行速度慢。VQ-VAE借鉴了自回归模型的思想,一个最明显的特征是通过encoder得到的隐变量是一个离散变量,将图像大小压缩到了一个小的特征空间。整体的流程大致如下图所示:
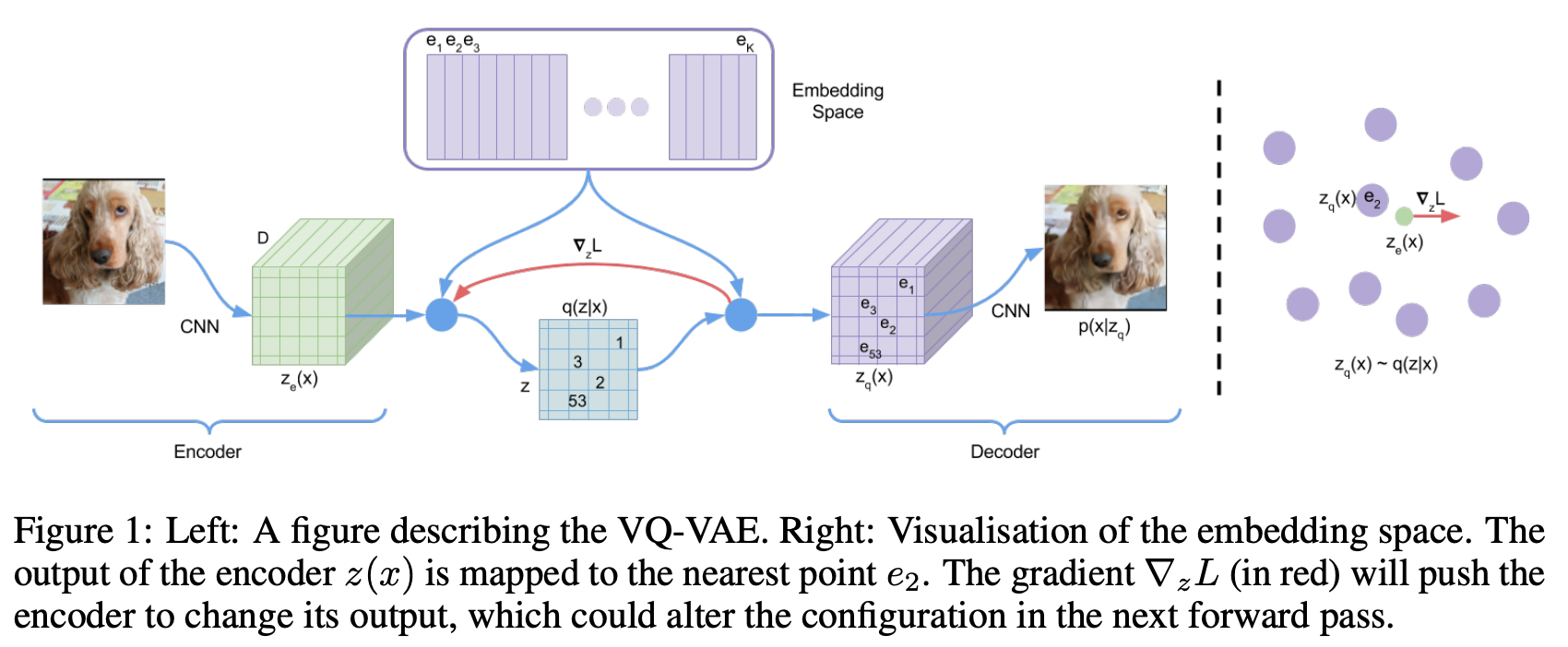
- 输入大小为\(H\times W\times 3\)的数据\(\mathbf{x}\),通过encoder得到初步的中间变量\(\mathbf{z}=\text{encoder}(\mathbf{x})\),大小缩小为\(h\times w\times d\)
- 模型会维护一个embedding层\(\mathbf{E}=[\mathbf{e}_1, \mathbf{e}_2, \dots, \mathbf{e}_K]\),即codebook,其中每个\(\mathbf{e}_i\)的长度都是\(d\)。对于\(\mathbf{z}\)中的每个\(d\),通过最近邻搜索得到相应的\(\mathbf{e}_i\)值,即有映射关系\(\mathbf{z}_q(\mathbf{x}) =\mathbf{e}_{argmin_j\vert\vert \mathbf{z}(\mathbf{x})-\mathbf{e}_j\vert\vert_2}\)。得到的编码向量用\(\mathbf{z}_q\)来表示,这样的编码向量其实就是一个离散向量
- 将\(\mathbf{z}_q\)输入到decoder中得到结果\(\hat{\mathbf{x}} = \text{decoder}(\mathbf{z}_q)\)
论文中给出了VQ-VAE的损失函数如下:
\[ L = -\log p(\mathbf{x}\vert\mathbf{z}_q(\mathbf{x}))+\vert\vert\text{sg}[\mathbf{z}(\mathbf{x})]-\mathbf{z}_q(\mathbf{x})\vert\vert_2^2+\beta\vert\vert\mathbf{z}(\mathbf{x})-\text{sg}[\mathbf{z}_q(\mathbf{x})]\vert\vert_2^2 \]
其中第一项是用来优化encoder和decoder的,即重建损失,从图中也可以看出,损失函数对\(\mathbf{z}\)的梯度是会推给encoder的。这一项通常是重建图像与输入图像的MSE损失\(\vert\vert \mathbf{x}-\text{decoder}(\mathbf{z}_q)\vert\vert_2^2\)。
由于我们在前向计算中有用到\(\argmin\)这个操作,这个是没有梯度的。对此,作者采用了Straight-Through Estimator方法人为地设计一个梯度,即\(\vert\vert \mathbf{x}-\text{decoder}(\mathbf{z} + \text{sg}[\mathbf{z}_q-\mathbf{z}])\vert\vert_2^2\)。式子中的\(\text{sg}\)代表的是stop gradient,即在反向传播时为0,前向计算为原值,数学描述如下:
\[ \text{sg}(x) = \begin{cases} x \quad \text{in forward process} \\ 0 \quad \text{backward process} \end{cases} \]
损失函数的后面两项与codebook有关。通常我们会希望\(\mathbf{z}_q\)与\(\mathbf{z}\)尽可能地靠近,所以优化目标是\(\vert\vert\mathbf{z}_q - \mathbf{z}\vert\vert_2^2\)。由于这个目标的梯度等于对\(\mathbf{z}\)的梯度加上对\(\mathbf{z}_q\)的梯度,所以我们可以将它等价为如下形式:
\[ \vert\vert\text{sg}[\mathbf{z}]-\mathbf{z}_q\vert\vert_2^2 + \vert\vert\mathbf{z}-\text{sg}[\mathbf{z}_q]\vert\vert_2^2 \]
等价在这里是指梯度等价,实际前向计算出来的loss值会是原来的两倍。上面式子中,第一项是\(\mathbf{z}_q\)的梯度,相当于固定\(\mathbf{z}\),让\(\mathbf{z}_q\)靠近\(\mathbf{z}\);而第二项是\(\mathbf{z}\)的梯度,相当于固定\(\mathbf{z}_q\),让\(\mathbf{z}\)靠近\(\mathbf{z}_q\)。因为\(\mathbf{z}_q\)相对于\(\mathbf{z}\)来说更自由一些,\(\mathbf{z}\)是encoder的输出,为了尽力保证重建后的效果,应该尽量让\(\mathbf{z}_q\)去靠近\(\mathbf{z}\)。这一步可以用权重去调整损失各项的重要性。
综上,VQ-VAE最终损失函数如下:
\[ L = \vert\vert \mathbf{x}-\text{decoder}(\mathbf{z} + \text{sg}[\mathbf{z}_q-\mathbf{z}])\vert\vert_2^2 + \gamma\vert\vert\text{sg}[\mathbf{z}]-\mathbf{z}_q\vert\vert_2^2 +\beta \vert\vert\mathbf{z}-\text{sg}[\mathbf{z}_q]\vert\vert_2^2 \]
其中\(\beta \lt \gamma\),论文中选取\(\gamma = 1\),\(\beta = 0.25\)。
从上面的描述中,我们可以看出VQ-VAE其实跟VAE并没有太大关系,它只是一个AE模型,目标在于图像重建。
在VQ-VAE论文中,作者利用PixelCNN去预测\(\mathbf{z}_q\),实现了随机图像的生成。训练时模型是共同训练VQ-VAE和PixelCNN的,输入数据通过encoder得到\(\mathbf{z}\),查询codebook得到\(\mathbf{z}_q\),再经过PixelCNN得到与\(\mathbf{z}_q\)同大小的变量\(\mathbf{z}_p\)作为decoder的输入。而在推理阶段则是直接将空图像输入到PixelCNN中得到\(\mathbf{z}_p^\prime\),之后直接输入到decoder中生成图像。
关于PixelCNN模型,可以参考这篇文章。